Динамическая система: различия между версиями
| Строка 90: | Строка 90: | ||
==Примеры непрерывных и дискретных систем== | ==Примеры непрерывных и дискретных систем== | ||
| − | '''Пример: модель Мальтуса'''. [[Файл:Мальтус.png|мини|]] | + | '''Пример: модель Мальтуса'''. [[Файл:Мальтус.png|мини|Рост популяции и ресурсов]] |
$$\quad$$''Модель Мальтуса'' — это экспоненциальный рост с постоянным темпом. Модель названа в честь английского демографа и экономиста [https://www.bing.com/ck/a?!&&p=fe40d8720325643eJmltdHM9MTcwMTgyMDgwMCZpZ3VpZD0xMWUxY2NjOS0xNjEyLTZjNWUtMzM5NC1jMzI1MTczYTZkNmImaW5zaWQ9NTE2Mw&ptn=3&ver=2&hsh=3&fclid=11e1ccc9-1612-6c5e-3394-c325173a6d6b&psq=%d0%a2%d0%be%d0%bc%d0%b0%d1%81%d0%b0+%d0%9c%d0%b0%d0%bb%d1%8c%d1%82%d1%83%d1%81%d0%b0.&u=a1aHR0cHM6Ly9ydS53aWtpcGVkaWEub3JnL3dpa2kvJUQwJTlDJUQwJUIwJUQwJUJCJUQxJThDJUQxJTgyJUQxJTgzJUQxJTgxLF8lRDAlQTIlRDAlQkUlRDAlQkMlRDAlQjAlRDElODFfJUQwJUEwJUQwJUJFJUQwJUIxJUQwJUI1JUQxJTgwJUQxJTgy&ntb=1 Томаса Мальтуса]. | $$\quad$$''Модель Мальтуса'' — это экспоненциальный рост с постоянным темпом. Модель названа в честь английского демографа и экономиста [https://www.bing.com/ck/a?!&&p=fe40d8720325643eJmltdHM9MTcwMTgyMDgwMCZpZ3VpZD0xMWUxY2NjOS0xNjEyLTZjNWUtMzM5NC1jMzI1MTczYTZkNmImaW5zaWQ9NTE2Mw&ptn=3&ver=2&hsh=3&fclid=11e1ccc9-1612-6c5e-3394-c325173a6d6b&psq=%d0%a2%d0%be%d0%bc%d0%b0%d1%81%d0%b0+%d0%9c%d0%b0%d0%bb%d1%8c%d1%82%d1%83%d1%81%d0%b0.&u=a1aHR0cHM6Ly9ydS53aWtpcGVkaWEub3JnL3dpa2kvJUQwJTlDJUQwJUIwJUQwJUJCJUQxJThDJUQxJTgyJUQxJTgzJUQxJTgxLF8lRDAlQTIlRDAlQkUlRDAlQkMlRDAlQjAlRDElODFfJUQwJUEwJUQwJUJFJUQwJUIxJUQwJUI1JUQxJTgwJUQxJTgy&ntb=1 Томаса Мальтуса]. | ||
| Строка 107: | Строка 107: | ||
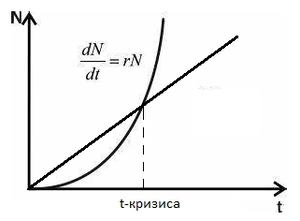
$$\quad$$Заметим, что при линейном распределении ресурсов, в модели Мальтуса существует точка кризиса ресурсов, когда их перестает хватать на популяцию, поэтому существует множество усовершенствованных моделей учитывающих этот фактор. Например, можно сделать коэффициент r (m) зависимым от времени или использовать модель с [https://ru.wikipedia.org/wiki/%D0%9B%D0%BE%D0%B3%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5 логистическим уравнением]. | $$\quad$$Заметим, что при линейном распределении ресурсов, в модели Мальтуса существует точка кризиса ресурсов, когда их перестает хватать на популяцию, поэтому существует множество усовершенствованных моделей учитывающих этот фактор. Например, можно сделать коэффициент r (m) зависимым от времени или использовать модель с [https://ru.wikipedia.org/wiki/%D0%9B%D0%BE%D0%B3%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5 логистическим уравнением]. | ||
| − | '''Пример: Задача о росте числа кроликов'''[[Файл:Поколения.png|мини|]] | + | '''Пример: Задача о росте числа кроликов'''[[Файл:Поколения.png|мини|Поколения кроликов]] |
$$\quad$$Одной из старейших и известнейших задач популяционной динамики является задача о росте числа кроликов. В этой задаче предполагается, что каждая пара кроликов через месяц после своего рождения производит другую пару кроликов, и рождение кроликов начинается со второго месяца. Эта задача была опубликована в 1202 году в "Трактате о счете" итальянского математика | $$\quad$$Одной из старейших и известнейших задач популяционной динамики является задача о росте числа кроликов. В этой задаче предполагается, что каждая пара кроликов через месяц после своего рождения производит другую пару кроликов, и рождение кроликов начинается со второго месяца. Эта задача была опубликована в 1202 году в "Трактате о счете" итальянского математика | ||
| Строка 123: | Строка 123: | ||
\end{cases} | \end{cases} | ||
\end{equation*} | \end{equation*} | ||
| − | |||
==Вопросы теории динамических систем== | ==Вопросы теории динамических систем== | ||
Версия 17:18, 6 декабря 2023
Динамическая система - это абстрактная математическая модель, которая состоит из множества элементов, связанных между собой функциональной зависимостью между временем и положением в фазовом пространстве каждого элемента системы. Такая модель позволяет изучать и описывать эволюцию системы во времени, что находит широкое применение в различных областях науки и техники.
Определение динамической системы является математической формализацией общей научной концепции детерминированного процесса. Процесс называется детерминированным, если весь его будущий ход и все его прошлое однозначно определяются состоянием в настоящее время.
Содержание
Введение
$$\quad$$ Динамическая система может быть представлена как система, которая имеет состояние. Подход, основанный на состоянии, позволяет описать динамику процесса, который является переходом системы из одного состояния в другое. Фазовое пространство системы представляет собой набор всех допустимых состояний динамической системы. Таким образом, динамическая система характеризуется своим начальным состоянием и законом, определяющим переход системы из начального состояния в другое.
$$\quad$$ Основная задача теории динамических систем - это исследование поведения систем, определяемых дифференциальными уравнениями. Это включает разбиение фазового пространства на траектории и изучение предельного поведения этих траекторий, таких как поиск и классификация положений равновесия, выделение притягивающих (аттракторы) и отталкивающих (репеллеры) множеств. Важнейшими понятиями теории динамических систем являются устойчивость состояний равновесия (способность системы при малых изменениях начальных условий оставаться около положения равновесия или на заданном множестве) и грубость (сохранение свойств при малых изменениях самой математической модели). Основные методы изучения динамических систем включают численное и аналитическое решение дифференциальных уравнений, а также геометрические методы анализа фазовых портретов.
Примеры
Пример 1.
$$\quad$$ Рассмотрим изолированную популяцию, находящуюся в неизменных условиях, не подвергающуюся внешнему воздействию, каждая особь которой имеет одинаковый доступ к ресурсам, а так же, одинаковую вероятность встретить (и таким образом конкурировать) другую особь популяции.
$$\quad$$ Так как численность не может быть отрицательной, то пространство состояний в данном примере $$X = \mathbb{R}^+$$, где $$\mathbb{R}^+ = \{N ∈ \mathbb{R}: N > 0\}$$. Здесь следует отметить, что если рассматривать численность как функцию времени, то очевидно, что эта функция целочисленна, т.е. $$N(t) ∈ {N ∈ Z: N > 0}$$. Величина $$\dfrac{N(t + ∆t) − N(t)}{∆t}$$ описывает среднюю скорость роста в интервале времени $$(t, t+∆t]$$. Если численность популяции велика, то скачки, вызванные рождением и смертью отдельных индивидуумов, выглядят пренебрежимо малыми на графике функции $$N(t)$$. Поэтому мы постулируем существование производной по времени $$\dfrac{dN(t)}{dt} = \lim\limits_{∆t→0}\dfrac{N(t + ∆t) − N(t)}{∆t} ≡ \dot{N}$$.
$$\quad$$Величина $$\dfrac{\dot{N}}{N}$$ показывает средний вклад одного индивидуума в популяционный рост.
Пример 2 (Экологическая система).
$$\quad$$ Состояние экологического сообщества в пределах определенной области $$Ω$$ может быть описано вектором с неотрицательными компонентами $$N = (N_1, N_2, . . . , N_n) ∈ \mathbb{R}^n_+$$, где $$N_i$$ — численность или плотность $$i$$-го вида. Здесь, очевидно, $$\mathbb{R}^n_+ = \{N ∈ \mathbb{R}^n: N > 0\}$$, где запись $$N > 0$$ для вектора $$N$$ обозначает, что $$N_i > 0$$ для всех $$i$$.
Пример 3.
$$\quad$$ В случае примера 1, можно добавить в рассмотрение признаки особей. Предположим, что распределение по признаку непрерывно (скажем, если признак — вес индивидуума или его возраст). Если обозначить пространство признаков как $$Γ$$, то состояние системы описывается функцией $$N(γ, t), γ ∈ Γ$$.
$$\quad$$ Отметим, что существуют два класса признаков, которые определяют неоднородность в популяции. Во-первых, это структурные признаки, такие как пространственное распределение и возраст, которые изменяются со временем для каждой особи в популяции. Во-вторых, существуют неизменные признаки, такие как генетическая предрасположенность к определенному заболеванию, которые остаются неизменными для каждой особи на протяжении ее жизни
Эволюционный оператор
Эволюция динамической системы означает изменение состояния системы со временем $$t ∈ T$$, где $$T$$ — упорядоченное множество.
$$\quad$$В математической биологии применяются два типа динамических систем: непрерывные с временем $$T = \mathbb{R}$$ и дискретные с целочисленным временем $$T = Z$$.
$$\quad$$Основным компонентом любой динамической системы является закон эволюции, который определяет состояние системы $$x_t$$ в момент времени $$t$$, при условии, что начальное состояние $$x_0$$ известно.
$$\quad$$Самый общий способ описать закон эволюции — задать отображение: \[ϕ^t: X → X,\] которое переводит начальное состояние в состояние системы в момент $$t$$: $$x_t = ϕ^t x_0$$.
$$\quad$$Отображение $$ϕ^t$$ часто называют эволюционным оператором динамической системы. Эволюционный оператор имеет два естественных свойства, которые отражают детерминированный характер поведения динамической системы: \begin{equation} \label{eq:0} ϕ^0 x = x,\ \forall x \in X,\\ \end{equation} \begin{equation} \label{eq:1} ϕ^{t+s} = ϕ^t◦ϕ^s\ \text{или}\ ϕ^{t+s}x = ϕ^t(ϕ^sx),\ \forall x \in X. \end{equation} $$\quad$$Другими словами, свойство \eqref{eq:0} означает, что динамическая система не изменяет своего состояния «спонтанно», а свойство \eqref{eq:1},что результат эволюции системы в течение $$t + s$$ единиц времени тот же самый, как если бы сначала зафиксировать изменение системы за $$s$$ единиц времени и затем получить состояние измененной системы еще через $$t$$ единиц времени.
Определение динамической системы
$$\quad$$Динамической системой называется пара $${X,\ ϕ^t}$$, где $$X$$ — пространство состояний, $$ϕ^t$$ — однопараметрическое семейство эволюционных операторов, удовлетворяющее свойствам \eqref{eq:0} и \eqref{eq:1}.
$$\quad$$Самый простой способ задать динамическую систему — указать эволюционный оператор в явном виде. Например, можно положить $$ϕ^1 = f(N) = 2N$$. То есть, за каждую единицу времени численность популяции увеличивается в 2 раза.
$$\quad$$Другой общий способ задания динамической системы — описать закон эволюции с помощью дифференциальных уравнений.
$$\quad$$Предположим, что пространство состояний динамической системы есть подмножество $$X = U ⊆ \mathbb{R}^n$$ с координатами $$u = (u_1, u_2, . . . , u_n)$$. Закон эволюции задается неявно, в терминах скоростей изменения координат: \[\dot{u} = f(u),\ u ∈ U ⊆ \mathbb{R}^n,\ f : U → \mathbb{R}^n,\] или, в покоординатной форме записи:
\begin{equation*} \begin{cases} \dot{u}_1 = f_1(u_1, u_2, . . . , u_n),\\ \dot{u}_2 = f_2(u_1, u_2, . . . , u_n),\\ ...\\ \dot{u}_n = f_n(u_1, u_2, . . . , u_n). \end{cases} \end{equation*}
Примеры непрерывных и дискретных систем
Пример: модель Мальтуса.
$$\quad$$Модель Мальтуса — это экспоненциальный рост с постоянным темпом. Модель названа в честь английского демографа и экономиста Томаса Мальтуса.
$$\quad$$Мальтузианские модели выглядят следующим образом: $$ N(t) = N_0e^{rt}$$, где
- N0 = N(0) — исходная численность населения,
- r — темп прироста населения («мальтузианский параметр»),
- t — время.
$$\quad$$В дискретном времени эту же модель можно записать в виде: $$N_{t+1} = mN_t$$, где m — константа пропорциональности.
$$\quad$$Заметим, что при линейном распределении ресурсов, в модели Мальтуса существует точка кризиса ресурсов, когда их перестает хватать на популяцию, поэтому существует множество усовершенствованных моделей учитывающих этот фактор. Например, можно сделать коэффициент r (m) зависимым от времени или использовать модель с логистическим уравнением.
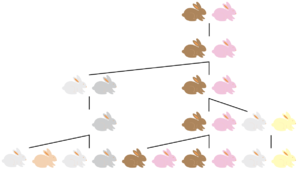
Пример: Задача о росте числа кроликов
$$\quad$$Одной из старейших и известнейших задач популяционной динамики является задача о росте числа кроликов. В этой задаче предполагается, что каждая пара кроликов через месяц после своего рождения производит другую пару кроликов, и рождение кроликов начинается со второго месяца. Эта задача была опубликована в 1202 году в "Трактате о счете" итальянского математика Леонардо Пизанского, более известного как Фибоначчи. Решением этой задачи является знаменитая последовательность чисел Фибоначчи. Математическая формулировка этой задачи выглядит следующим образом:
\[ N_{t+1} = N_t + N_{t-1}, \]
где $$N_t$$ - число пар кроликов в t-ый месяц, $$N_0 = 0,\ N_1 = 1$$.
$$\quad$$Т. е. динамическая система может выглядеть следующим образом: \begin{equation*} \begin{cases} M_{t+1} = N_t,\\ N_{t+1} = N_t+M_t. \end{cases} \end{equation*}
Вопросы теории динамических систем
$$\quad$$Имея какое-то задание динамической системы, далеко не всегда можно найти и описать её траектории в явном виде. Поэтому обычно рассматриваются более простые (но не менее содержательные) вопросы об общем поведении системы. Например:
- Есть ли у системы замкнутые фазовые кривые, то есть может ли она вернуться в начальное состояние в ходе эволюции?
- Как устроен аттрактор системы, то есть множество в пространстве состояний, к которому стремится «большинство» траекторий?
- Как ведут себя траектории, выпущенные из близких точек — остаются ли они близкими или уходят со временем на значительное расстояние?
- Что можно сказать о поведении «типичной» динамической системы из некоторого класса?
- Что можно сказать о поведении динамических систем, «близких» к данной?
См. также
- Неподвижные точки системы
- Дискретные системы с запаздыванием
- Модель динамики популяции жуков (Tribolium)
- Гамильтоновы системы
- Система Лотки-Вольтерры. Принцип Вольтерры
Список литературы
- Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии 2011.
- Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2023.