Отделимость множеств: различия между версиями
Oleg23 (обсуждение | вклад) |
Oleg23 (обсуждение | вклад) |
||
| Строка 2: | Строка 2: | ||
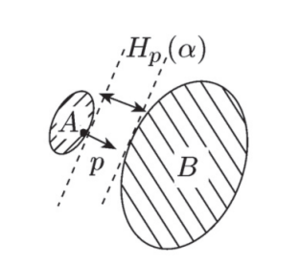
[[Файл:Отделимость выпуклых множеств.png|мини|Пример отделимых выпуклых множеств.]] | [[Файл:Отделимость выпуклых множеств.png|мини|Пример отделимых выпуклых множеств.]] | ||
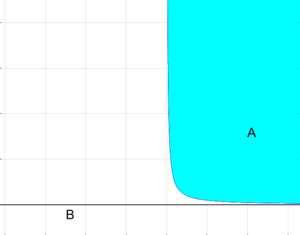
| + | [[Файл:Сильная отделимость.png|мини|Сильная отделимость множеств]] | ||
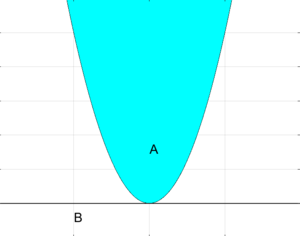
| + | [[Файл:Строгая отделимость множеств.png|мини|Строгая отделимость множеств]] | ||
| + | [[Файл:Нестрогая отделимость множеств.png|мини|Нестрогая отделимость множеств]] | ||
Дадим сперва необходимые определения. | Дадим сперва необходимые определения. | ||
Версия 20:16, 11 ноября 2023
Для получения многих результатов в выпуклом анализе ключевую роль занимают теоремы об отделимости выпуклых множеств.
Дадим сперва необходимые определения.
Определения
Определение 1. Аффинной комбинацией точек $$x_1, x_2, \ldots, x_n \in X$$ назовём выражение $$\sum_{i = 1} ^ n \alpha_i x_i$$, где числа $$\alpha_1, \alpha_2, \ldots, \alpha_n$$ удовлетворяют условию $$\sum_{i = 1} ^ n \alpha_i = 1$$.
Определение 2. Аффинной оболочкой множества $$A$$ назовём множество всевозможных аффинных комбинаций точек множества $$A: \, aff A := \{\sum_{i = 1} ^ n \alpha_i x_i \, | \, n \in \mathbb N, \, x_1, \, x_2, \ldots, x_n \in X, \, \sum_{i = 1} ^ n \alpha_i = 1\}$$.
Определение 3. Относительной внутренностью множества $$A$$ назовём его «внутренность относительно аффинной оболочки $$A$$», то есть множество точек $$ri \, A := \{x \in X \, | \, \exists \varepsilon > 0: O(x, \, \varepsilon) \cap aff A \subset A\}$$. Здесь $$ O(x, \, \varepsilon) = \{y \in X \, | \, ||y - x|| < \varepsilon \}$$ - открытый шар в нормированном пространстве $$X$$.
Определение 4 (Отделимость в конечномерных пространствах). Пусть $$X$$ - конечномерное пространство, множества $$A, \, B \subset X$$. Будем говорить, что множества $$A$$ и $$B$$ отделимы, если найдётся такой действующий на $$X$$ линейный непрерывный функционал $$l \not= 0$$, что \begin{gather*} \sup\limits_{x \in A}\left<l, x\right>\leq\inf\limits_{y \in B}\left<l, y\right>. \end{gather*} Также говорят, что функционал $$l$$ разделяет множества $$A$$ и $$B$$. Если вдобавок оказалось, что \begin{gather*} \sup\limits_{x \in A}\left<l, x\right><\inf\limits_{y \in B}\left<l, y\right>, \end{gather*}
то говорят, что множества $$A$$ и $$B$$ строго отделимы.
Определение 5 (Отделимость в бесконечномерных пространствах). Пусть $$X = (X, \, ||\cdot||)$$ - банахово пространство, множества $$A, \, B \subset X$$. Будем говорить, что множества $$A$$ и $$B$$ отделимы, если найдётся такой действующий на $$X$$ линейный функционал $$l \not= 0$$, что \begin{gather*} \sup\limits_{x \in A}\left<l, x\right>\leq\inf\limits_{y \in B}\left<l, y\right>. \end{gather*} Также говорят, что функционал $$l$$ разделяет множества $$A$$ и $$B$$. Если вдобавок оказалось, что \begin{gather*} \sup\limits_{x \in A}\left<l, x\right><\inf\limits_{y \in B}\left<l, y\right>, \end{gather*}
то говорят, что множества $$A$$ и $$B$$ строго отделимы.
Это определение отличается от определения 4, ведь непрерывность функционала $$l$$ здесь не требуется. В определениях 4 и 5 не требуется выпуклость множеств $$A, \, B$$, однако утверждения ниже, как и другие результаты в отделимости множеств, доказываются в предположении их выпуклости.
Определение 6. Пусть $$X = (X, \, \rho)$$ - вещественное нормированное пространство. Функционал $$p: X \to \mathbb R$$ назовём однородно-выпуклым, если \begin{gather*} p(\lambda x) = \lambda x \; \forall \lambda \geqslant 0, \; p(x + y) \leqslant p(x) + p(y) \; \forall x, \, y \in X. \end{gather*}
Теоремы отделимости
Начнём с важного результата в функциональном анализе - теоремы Хана-Банаха.
Теорема 1 (Hans Hahn, Stefan Banach). Пусть $$p$$ - однородно-выпуклый функционал на вещественном нормированном пространстве $$X = (X, \, ||\cdot||)$$. Пусть $$X_0 \subset X$$ - линейное подпространство, причём на $$X_0$$ задан линейный функционал $$f_0: X_0 \to \mathbb R$$, подчинённый функционалу $$p$$ (это означает, что $$f_0(x) \leqslant p(x) \; \forall x \in X_0$$). Тогда существует продолжение $$f$$ функционала $$f_0$$ с подпространства $$X_0$$ на всё пространство $$X$$, причём функционал $$f$$ подчинён функционалу $$p$$: \begin{gather*} f(x) \leqslant p(x) \; \forall x \in X. \end{gather*}
Предложение 1. Множества $$A, \, B$$ можно отделить тогда и только тогда, когда множество $$A − B$$ (имеется в виду сумма по Минковскому множеств $$A$$ и $$-B$$, то есть множество $$\{a - b \, | \, a \in A, \, b \in B \}$$) можно отделить от $$\{0\}$$ (множества, состоящего из одного нуля).
Доказательство.
1. Необходимость. Пусть множества $$A, \, B$$ отделимы. Это означает, что $$\exists l \not= 0$$ - линейный непрерывный функционал на $$X$$ такой, что \begin{gather*} \sup\limits_{x \in A}\left<l, x\right>\leq\inf\limits_{y \in B}\left<l, y\right>. \end{gather*} То есть \begin{gather*} \forall x \in X \; \forall y \in Y \left<l, x\right> \leq \left<l, y\right>, \end{gather*} что означает: \begin{gather*} \forall x \in X \; \forall y \in Y \left<l, x - y\right> \leq 0 = \left<l, 0\right>, \end{gather*} или \begin{gather*} \sup_{z \in A - B} \left<l, z\right> \leq 0 = \inf_{z \in \{0\}} \left<l, z\right>. \end{gather*} Последнее неравенство эквивалентно отделимости множества $$A - B$$ от множества $$\{0\}$$.
2. Достаточность. Пусть множество $$A - B$$ отделимо от нуля. Тогда $$\exists l \not= 0$$ - линейный непрерывный функционал на $$X$$ такой, что \begin{gather*} \sup_{z \in A - B} \left<l, z\right> \leq 0 = \left<l, 0\right>, \end{gather*} то есть \begin{gather*} \sup_{z \in A - B} \left<l, z\right> \leq 0 = \left<l, 0\right>, \end{gather*} и поскольку $$\sup (A - B) = \sup A -\inf B$$, то заключаем \begin{gather*} \sup\limits_{x \in A}\left<l, x\right>\leq\inf\limits_{y \in B}\left<l, y\right>. \end{gather*} Последнее неравенство эквивалентно отделимости множеств $$A$$ и $$B$$. $$~~\blacksquare$$
Этим фактом мы воспользуемся при доказательстве следующей теоремы. Предпошлем доказательству одну лемму.
Лемма 1. Пусть непустое множество $$C \subset \mathbb R ^ n$$ выпукло, причём $$0 \not \in int \, C$$. Тогда $$C$$ отделимо от нуля.
Доказательство. Рассмотрим выпуклое замкнутое множество $$\overline C$$. Понятно, что нуль не принадлежит внутренности $$int \, \overline C$$, поскольку $$int \, C = int \, \overline C$$. Поэтому либо нуль не принадлежит множеству $$\overline C$$, либо принадлежит его границе $$\partial \overline C$$. Значит, в любом случае существует последовательность $$x_i \to 0, \, x_i \not \in \overline C \, \forall i$$. Рассмотрим множества $$C_i := \overline C - x_i$$. Имеем $$0 \not \in C_i \, \forall i$$. Каждое из этих непустых выпуклых замкнутых множеств $$C_i$$ можно отделить от нуля. Следовательно, для $$\forall i$$ существуют числа $$l_i \in \mathbb R$$ такие, что $$\left< l_i, \eta \right> \geqslant 0 \, \forall \eta \in C_i$$. Нормируем каждый вектор $$l_i$$. Тогда все эти векторы единичные. Перейдём (по теореме Больцано-Вейерштрасса) от ограниченной последовательности $$(l_i)$$ к сходящейся подпоследовательности $$(l_{i_k})$$, обозначим $$l = \lim_{k \to +\infty} l_{i_k}, \, l \not= 0$$. Из определения множеств $$C_i$$ и неравенства Коши-Буняковского: \begin{gather*} \left< l_i, x \right> + |l_i| |x_i| \geqslant 0 \, \forall x \in \overline C \; \forall i. \end{gather*} Зафиксируем $$x \in \overline C$$, и, переходя в полученных неравенствах к пределу при $$i \to +\infty$$, получим $$\left< l, x \right> \geqslant 0$$. В силу произвольности выбора $$x$$ мы получаем, что $$C$$ отделимо от нуля. $$~~\blacksquare$$
Теорема 1. (Об отделимости в конечномерном пространстве). Пусть $$A, B$$ — непустые выпуклые подмножества $$\mathbb R^n$$ и их относительные внутренности $$ri \, A$$ и $$ri \, B$$ не пересекаются. Тогда множества $$A$$ и $$B$$ можно отделить.
Доказательство. Заметим, что так как $$ri \, A \cap ri \, B = \emptyset$$, то $$0\not\in (ri \, A - ri \, B)$$. Множество $$(ri \, A - ri \, B)$$ выпукло $$\Longrightarrow$$ $$(ri \, A - ri \, B)$$ отделимо от нуля в силу Леммы 1, а значит, $$ri \, A$$ и $$ri \, B$$ отделимы, то есть на $$X$$ существует линейный непрерывный функционал $$l \not= 0$$ и число $$\gamma \in \mathbb R: \forall x \in {ri \, A} \; \forall y \in {ri \, B} \Longrightarrow\left<l, x\right>\leq\gamma\leq\left<l, y\right>$$.
Пусть $$x \in A$$. Тогда существует последовательность точек $$\{x_i\}$$, лежащая в $$ri A$$ и сходящаяся к $$x$$. Поэтому, $$\left<l, x_i\right>\leq\gamma,$$ $$\forall i$$. Переходя к пределу по $$i$$, получаем, что, $$\left<l, x\right>\leq\gamma$$. Поступив аналогично для точек $$y$$ множества $$B$$, получим, что полученный линейный непрерывный функционал $$l$$ также разделяет $$A$$ и $$B$$.$$~~\blacksquare$$
Теперь перейдём к бесконечномерному пространству $$X$$. Отделимость множеств в $$X$$ имеет существенные отличия от отделимости множеств в $$\mathbb R ^ n$$, что показывает следующий пример.
Пример 1. В бесконечномерном пространстве $$l_2$$ числовых последовательностей $$(x_1, \, x_2, \, \ldots, \, x_n, \, \ldots)$$, для которых ряд $$\sum_{i = 1} ^ {+\infty} x_i ^ 2 < \infty$$, рассмотрим множество П $$= \{x = (x_1, \, x_2, \, \ldots, \, x_n, \, \ldots) \, | \, |x_i| \leqslant 2 ^ {-i} \, \forall i \}$$ - гильбертов кирпич. Гильбертов кирпич содержит нуль (проверяется подстановкой последовательности $$(0, \, 0, \, \ldots, \, 0, \, \ldots)$$ в определение П), является выпуклым компактом, не лежит ни в каком конечномерном пространстве. Далее, $$int$$ П не содержит нуля. Действительно, предположим противное: пусть $$0 \in int$$ П. Тогда $$\exists \varepsilon > 0: B(0, \, \varepsilon) = \{x \in l_2 \, | \, ||x||_{l_2} \leqslant \varepsilon\} \subset$$ П. Выберем число $$j = \Big \lfloor \log_2 \displaystyle \frac{1}{\varepsilon} \Big \rfloor + 1$$. Тогда $$2 ^ {-j} < 2 ^ {-\log_2 \frac{1}{\varepsilon}} = \varepsilon$$. Но последовательность $$y = (0, \, 0, \, \ldots, \, \varepsilon, \, \ldots)$$, где компонента $$\varepsilon$$ - с номером $$j$$, имеет норму $$||y|| = \sqrt{\sum_{i = 1} ^ {+\infty} y_i ^ 2} = \varepsilon \Rightarrow y \in B(0, \, \varepsilon), \, y \in$$ П, ведь $$|y_j| = \varepsilon > 2 ^ {-j}$$. Полученное противоречие доказывает, что $$int$$ П не содержит нуля.
Докажем, что П не отделимо от множества $$\{ 0 \}$$. Заметим в скобках, что в конечномерном пространстве отделимость выпуклого множества с внутренностью, не содержащей нуля, была бы гарантирована Леммой 1.
Действительно, предположим противное: пусть множества П и $$\{0\}$$ отделимы. Тогда существует разделяющий их ненулевой линейный функционал $$l \in l_2 ^ {*} = l_2$$ (здесь $$l_2 ^ {*}$$ - пространство, сопряженное к $$l_2$$; из курса функционального анализа известно, что $$l_2 ^ {*} = l_2$$). Имеем \begin{equation} \label{eq1} \left< l, \, x \right> \geqslant 0 \; \forall x \in П. \end{equation} Рассмотрим две последовательности векторов $$e_i ^ {+} = (0, \, 0, \, \ldots, \, 0, \, 2 ^ {-i}, \, 0, \, \ldots)$$ и $$e_i ^ {-} = (0, \, 0, \, \ldots, \, 0, \, -2 ^ {-i}, \, 0, \, \ldots)$$, где $$i \in \mathbb N$$, а единственная ненулевая компонента векторов $$e_i ^ {+}, \, e_i ^ {-}$$ имеет номер $$i$$. Подставим векторы из этой последовательности в \eqref{eq1}. Получим, что если функционал $$l = (l_1, \, l_2, \, \ldots, \, l_n, \, \ldots)$$, то из $$\left< l, \, e_i ^ {+} \right> = l_i 2 ^ {-i} \geqslant 0, \, \left< l, \, e_i ^ {-} \right> = -l_i 2 ^ {-i} \geqslant 0$$ следует $$l_i = 0 \; \forall i$$, и значит, $$l = 0$$.
Сформулируем достаточные условия отделимости и строгой отделимости множеств в бесконечномерном пространстве.
Теорема 2. (Об отделимости в бесконечномерном пространстве). Пусть $$M, \, N$$ - непустые выпуклые подмножества $$X, \, int \, M \not= \emptyset$$ и $$int \, M \cap N = \emptyset$$. Тогда множества $$M$$ и $$N$$ можно отделить.
Теорема 3. (О строгой отделимости в бесконечномерном пространстве). Пусть $$A, \, B$$ - непустые выпуклые подмножества $$X, \, A \cap B = \emptyset, \; A$$ компактно, а $$B$$ замкнуто. Тогда множества $$A$$ и $$B$$ можно строго отделить.
Доказательство.