Теорема Каратеодори: различия между версиями
German22 (обсуждение | вклад) |
German22 (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | Будем рассматривать множество $$X$$ - | + | Будем рассматривать множество $$X$$ $$-$$ вещественное линейное пространство и $$A \subset X$$.<br> |
'''Выпуклой оболочкой множества $$A$$''' множества называется пересечение всех выпуклых множеств, содержащих $$A$$, и обозначается $$\operatorname{conv} A$$.<br> | '''Выпуклой оболочкой множества $$A$$''' множества называется пересечение всех выпуклых множеств, содержащих $$A$$, и обозначается $$\operatorname{conv} A$$.<br> | ||
| − | '''Симплекс''' - | + | '''Симплекс''' $$-$$ геометрическая фигура, являющаяся $$n-$$мерным обобщением треугольника. |
| − | Рассмотрим теорему Каратеодори, которая утверждает, что если точка $$x$$ лежит в выпуклой оболочке подмножества $$A$$ евклидового пространства, то найдётся невырожденный симплекс с вершинами в $$A$, содержащий x. | + | Рассмотрим теорему Каратеодори, которая утверждает, что если точка $$x$$ лежит в выпуклой оболочке подмножества $$A$$ евклидового пространства, то найдётся невырожденный симплекс с вершинами в $$A$$, содержащий x. |
== Теорема Каратеодори == | == Теорема Каратеодори == | ||
Пусть $$A \subset \mathbb{R}^n$$. Тогда $$\operatorname{conv} A$$ состоит из всевозможных выпуклых комбинаций не более чем $$(n+1)$$ точек множества $$A$$. | Пусть $$A \subset \mathbb{R}^n$$. Тогда $$\operatorname{conv} A$$ состоит из всевозможных выпуклых комбинаций не более чем $$(n+1)$$ точек множества $$A$$. | ||
===== Доказательство ===== | ===== Доказательство ===== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Положим | Положим | ||
\begin{gather*} | \begin{gather*} | ||
| Строка 67: | Строка 44: | ||
Для случая $$n = 2$$ множество $$A \subset \mathbb{R}^2$$ - подмножество координатной плоскости, $$\operatorname{conv}(A)$$ — объединение всех треугольников с вершинами в $$A$$. | Для случая $$n = 2$$ множество $$A \subset \mathbb{R}^2$$ - подмножество координатной плоскости, $$\operatorname{conv}(A)$$ — объединение всех треугольников с вершинами в $$A$$. | ||
| − | |||
=== Визуализация случая $$n=2$$=== | === Визуализация случая $$n=2$$=== | ||
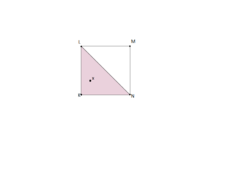
Рассмотрим набор точек $$A = \large((0,0), (0,1), (1,0), (1,1)\large)$$, который является подмножеством $$\mathbb{R}^2$$, $$\operatorname{conv} A$$ - квадрат. Рассмотрим теперь точку $$x = (\dfrac{1}{4}, \dfrac{1}{4})$$, $$x \in A$$. Построим теперь выпуклую оболочку, натянутую на множество точек $$A' = \large((0,0), (0,1), (1,0)\large)$$, $$\operatorname{conv} A'$$ - треугольник, и $$x \in A'$$. Таким образом, для двумерного случая, мы можем построить треугольник, состоящий из точек из $$A$$, который охватывает любую точку из $$A$$ | Рассмотрим набор точек $$A = \large((0,0), (0,1), (1,0), (1,1)\large)$$, который является подмножеством $$\mathbb{R}^2$$, $$\operatorname{conv} A$$ - квадрат. Рассмотрим теперь точку $$x = (\dfrac{1}{4}, \dfrac{1}{4})$$, $$x \in A$$. Построим теперь выпуклую оболочку, натянутую на множество точек $$A' = \large((0,0), (0,1), (1,0)\large)$$, $$\operatorname{conv} A'$$ - треугольник, и $$x \in A'$$. Таким образом, для двумерного случая, мы можем построить треугольник, состоящий из точек из $$A$$, который охватывает любую точку из $$A$$ | ||
| + | |||
| + | |||
| + | == Теорема о наполнении выпуклой оболочки == | ||
| + | Множество $$\operatorname{conv} A$$ состоит из тех и только тех точек, которые являются выпуклыми комбинациями конечного числа точек из $$A$$. | ||
| + | |||
| + | ==== Доказательство ==== | ||
| + | |||
| + | Обозначим через $$B$$ множество всевозможных выпуклых комбинаций конечного числа точек из $$A$$. Поскольку множество conv $$A$$ выпукло и $$A \subset \operatorname{conv} A$$, то $$B \subset$$ $$\operatorname{conv}$$ $$A$$. Докажем обратное включение.<br> | ||
| + | |||
| + | Покажем, что множество $$B$$ выпукло. <br> | ||
| + | Действительно, пусть $$b_1, b_2 \in B$$. Тогда каждая из точек $$b_1$$ и $$b_2$$ представима в виде выпуклой комбинации конечного числа точек из $$A$$, причем, увеличивая, если надо, число этих точек, можно без потери общности считать, что существуют номер $$m$$ и точки $$a_i \in A, i=\overline{1, m}$$, для которых справедливы представления $$b_s=\sum\limits_{i=1}^m \alpha_{s, i} a_i,~ s=1,2$$. Здесь $$\alpha_{s, i}, i=\overline{1, m}, s=1,2$$, - некоторые неотрицательные числа, для которых $$\sum\limits_{i=1}^m \alpha_{s, i}=1,~ s=1,2$$. Осталось доказать, что $$\theta b_1+(1-\theta) b_2 \in B ~~\forall \theta \in[0,1]$$. Действительно, | ||
| + | \begin{gather*} | ||
| + | \theta b_1+(1-\theta) b_2=\sum\limits_{i=1}^m\left(\theta \alpha_{1, i}+(1-\theta) \alpha_{2, i}\right)a_i \in B, | ||
| + | \end{gather*} | ||
| + | поскольку $$\theta \alpha_{1, i}+(1-\theta) \alpha_{2, i} \geqslant 0$$ для всех $$i$$ и | ||
| + | |||
| + | \begin{gather*} | ||
| + | \sum\limits_{i=1}^m\left(\theta \alpha_{1, i}+(1-\theta) \alpha_{2, i}\right)=\theta \sum\limits_{i=1}^m \alpha_{1, i}+(1-\theta) \sum\limits_{i=1}^m \alpha_{2, i}=\theta+(1-\theta)=1. | ||
| + | \end{gather*} | ||
| + | |||
| + | Таким образом, выпуклость множества $$B$$ доказана. В то же время, $$A \subset B$$ и, значит, conv $$A \subset B$$. Итак, равенство conv $$A=B$$ доказано. | ||
== Список литературы == | == Список литературы == | ||
| − | 1 | + | 1) Арутюнов А. В. "Лекции по выпуклому и многозначному анализу", М.: ФИЗМАТЛИТ, 2004. |
| − | |||
| − | |||
Версия 09:47, 23 октября 2022
Будем рассматривать множество $$X$$ $$-$$ вещественное линейное пространство и $$A \subset X$$.
Выпуклой оболочкой множества $$A$$ множества называется пересечение всех выпуклых множеств, содержащих $$A$$, и обозначается $$\operatorname{conv} A$$.
Симплекс $$-$$ геометрическая фигура, являющаяся $$n-$$мерным обобщением треугольника.
Рассмотрим теорему Каратеодори, которая утверждает, что если точка $$x$$ лежит в выпуклой оболочке подмножества $$A$$ евклидового пространства, то найдётся невырожденный симплекс с вершинами в $$A$$, содержащий x.
Содержание
Теорема Каратеодори
Пусть $$A \subset \mathbb{R}^n$$. Тогда $$\operatorname{conv} A$$ состоит из всевозможных выпуклых комбинаций не более чем $$(n+1)$$ точек множества $$A$$.
Доказательство
Положим
\begin{gather*}
B=\left\{x: x=\sum\limits_{i=1}^{n+1} \alpha_i x_i, \text { где } x_i \in A, ~\alpha_i \geqslant 0~\forall i=\overline{1, n+1}, \sum\limits_{i=1}^{n+1} \alpha_i=1\right\} \text {. }
\end{gather*}
По теореме о наполнении выпуклой оболочки(доказывается дальше) $$\operatorname{conv} A: B \subset \operatorname{conv} A$$. Осталось показать, что $$\operatorname{conv} A \subset B$$.
Пусть $$x \in \operatorname{conv} A$$. Тогда для некоторого натурального $$r$$ справедливо представление:
\begin{gather*} x=\sum\limits_{i=1}^{r+1} \alpha_i x_i,~~ \text{где } \alpha_i \geqslant 0, ~x_i \in A, ~i=\overline{1, r+1},~ \sum\limits_{i=1}^{r+1} \alpha_i=1. \end{gather*}
Если $$r \leqslant n$$, то $$x \in B$$. Пусть теперь $$r>n$$. Покажем, что в этом случае $$x$$ можно представить в виде выпуклой комбинации не более чем $$~r~$$ точек множества $$A$$. Если хотя бы одно из чисел $$\alpha_i$$ равно нулю, то это очевидно. Пусть теперь $$\alpha_i>0 ~\forall i$$. Поскольку $$r>n$$, система векторов $$x_i-x_{r+1},~ i=1, \ldots, r$$, линейно зависима. Поэтому найдутся такие числа $$t_1, \ldots, t_r$$, не все равные нулю, что
\begin{gather*} \sum\limits_{i=1}^r t_i\left(x_i-x_{r+1}\right)=0 \end{gather*}
Положим $$t_{r+1}=-\sum\limits_{i=1}^r t_i$$. Тогда $$\sum\limits_{i=1}^{r+1} x_i t_i=0, \sum\limits_{i=1}^{r+1} t_i=0$$ и, значит, для произвольного числа $$c$$ :
\begin{gather}\label{eq1} x=\sum\limits_{i=1}^{r+1} \alpha_i x_i+\sum\limits_{i=1}^{r+1} c t_i x_i=\sum\limits_{i=1}^{r+1}\left(\alpha_i+c t_i\right) x_i, \quad \sum\limits_{i=1}^{r+1}\left(\alpha_i+c t_i\right)=1. \end{gather}
Очевидно, хотя бы одно из чисел $$t_i$$ отрицательно. Кроме того, $$\alpha_i>0$$ для любого $$i$$ и, значит, при $$c=0$$ все числа $$\left(\alpha_i+c t_i\right)$$ положительны. Будем увеличивать параметр $$c$$ от нуля до бесконечности. Тогда, очевидно, существует наименьшее число $$c>0$$ такое, что для всех номеров $$i$$ выполняется $$\left(\alpha_i+c t_i\right) \geqslant 0$$, а для некоторого $$i_0 \leqslant r+1$$ имеет место $$\left(\alpha_{i_0}+c t_{i_0}\right)=0$$. Поэтому, отбрасывая в представлении (\ref{eq1}) $$i_0$$-е слагаемое $$\left(\alpha_{i_0}+c t_{i_0}\right) x_{i_0}$$, получаем искомое утверждение, т. е. что $$x$$ представимо в виде выпуклой линейной комбинации не более чем $$r$$ точек множества $$A$$.
Повторяя указанную процедуру конечное число раз, получим, что $$r \leqslant n$$ и, значит, $$x \in B$$. Таким образом, доказано, что $$\operatorname{conv} A \subset B$$
Следствия
Для случая $$n = 1$$ множество $$A\subset \mathbb{R}^1$$ - подмножество прямой, $$\operatorname{conv}(A)$$ — объединение всех отрезков с концами в $$A$$.
Для случая $$n = 2$$ множество $$A \subset \mathbb{R}^2$$ - подмножество координатной плоскости, $$\operatorname{conv}(A)$$ — объединение всех треугольников с вершинами в $$A$$.
Визуализация случая $$n=2$$
Рассмотрим набор точек $$A = \large((0,0), (0,1), (1,0), (1,1)\large)$$, который является подмножеством $$\mathbb{R}^2$$, $$\operatorname{conv} A$$ - квадрат. Рассмотрим теперь точку $$x = (\dfrac{1}{4}, \dfrac{1}{4})$$, $$x \in A$$. Построим теперь выпуклую оболочку, натянутую на множество точек $$A' = \large((0,0), (0,1), (1,0)\large)$$, $$\operatorname{conv} A'$$ - треугольник, и $$x \in A'$$. Таким образом, для двумерного случая, мы можем построить треугольник, состоящий из точек из $$A$$, который охватывает любую точку из $$A$$
Теорема о наполнении выпуклой оболочки
Множество $$\operatorname{conv} A$$ состоит из тех и только тех точек, которые являются выпуклыми комбинациями конечного числа точек из $$A$$.
Доказательство
Обозначим через $$B$$ множество всевозможных выпуклых комбинаций конечного числа точек из $$A$$. Поскольку множество conv $$A$$ выпукло и $$A \subset \operatorname{conv} A$$, то $$B \subset$$ $$\operatorname{conv}$$ $$A$$. Докажем обратное включение.
Покажем, что множество $$B$$ выпукло.
Действительно, пусть $$b_1, b_2 \in B$$. Тогда каждая из точек $$b_1$$ и $$b_2$$ представима в виде выпуклой комбинации конечного числа точек из $$A$$, причем, увеличивая, если надо, число этих точек, можно без потери общности считать, что существуют номер $$m$$ и точки $$a_i \in A, i=\overline{1, m}$$, для которых справедливы представления $$b_s=\sum\limits_{i=1}^m \alpha_{s, i} a_i,~ s=1,2$$. Здесь $$\alpha_{s, i}, i=\overline{1, m}, s=1,2$$, - некоторые неотрицательные числа, для которых $$\sum\limits_{i=1}^m \alpha_{s, i}=1,~ s=1,2$$. Осталось доказать, что $$\theta b_1+(1-\theta) b_2 \in B ~~\forall \theta \in[0,1]$$. Действительно,
\begin{gather*}
\theta b_1+(1-\theta) b_2=\sum\limits_{i=1}^m\left(\theta \alpha_{1, i}+(1-\theta) \alpha_{2, i}\right)a_i \in B,
\end{gather*}
поскольку $$\theta \alpha_{1, i}+(1-\theta) \alpha_{2, i} \geqslant 0$$ для всех $$i$$ и
\begin{gather*} \sum\limits_{i=1}^m\left(\theta \alpha_{1, i}+(1-\theta) \alpha_{2, i}\right)=\theta \sum\limits_{i=1}^m \alpha_{1, i}+(1-\theta) \sum\limits_{i=1}^m \alpha_{2, i}=\theta+(1-\theta)=1. \end{gather*}
Таким образом, выпуклость множества $$B$$ доказана. В то же время, $$A \subset B$$ и, значит, conv $$A \subset B$$. Итак, равенство conv $$A=B$$ доказано.
Список литературы
1) Арутюнов А. В. "Лекции по выпуклому и многозначному анализу", М.: ФИЗМАТЛИТ, 2004.