Теорема Каратеодори
Будем рассматривать $$n$$-мерное пространство $$X$$ — вещественное линейное пространство и $$A \subset X$$.
Выпуклой оболочкой множества $$A$$ множества называется пересечение всех выпуклых множеств, содержащих $$A$$, и обозначается $$\operatorname{conv} A$$.
Пусть векторы $$x_0 x_1, ..., x_n \in X$$ аффинно независимы. Множество $$S = \operatorname{conv} (x_0, x_1, ..., x_n)$$ называется $$n$$-мерным симплексом с вершинами $$x_0, x_1,..., x_n$$. В частности, вырожденный симплекс размера $$n$$ — симплекс размера $$n-1$$.
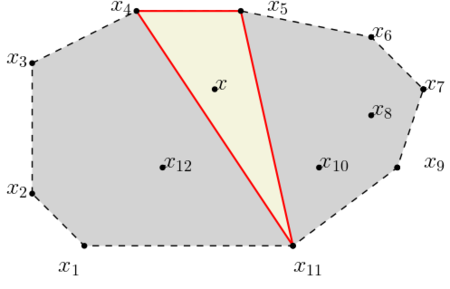
Рассмотрим теорему Каратеодори, которая утверждает, что если точка $$x$$ лежит в выпуклой оболочке подмножества $$A$$ евклидового пространства, то найдётся невырожденный симплекс с вершинами в $$A$$, содержащий $$x$$.
Теорема Каратеодори
Пусть $$A \subset \mathbb{R}^n$$. Тогда $$\operatorname{conv} A$$ состоит из всевозможных выпуклых комбинаций не более чем $$(n+1)$$ точек множества $$A$$.
Доказательство
Положим
\begin{gather*}
B=\left\{x: x=\sum\limits_{i=1}^{n+1} \alpha_i x_i, \text { где } x_i \in A, ~\alpha_i \geqslant 0~\forall i=\overline{1, n+1}, \sum\limits_{i=1}^{n+1} \alpha_i=1\right\} \text {. }
\end{gather*}
По теореме о наполнении выпуклой оболочки $$\operatorname{conv} A: B \subset \operatorname{conv} A$$. Осталось показать, что $$\operatorname{conv} A \subset B$$.
Пусть $$x \in \operatorname{conv} A$$. Тогда для некоторого натурального $$r$$ справедливо представление:
\begin{gather*} x=\sum\limits_{i=1}^{r+1} \alpha_i x_i,~~ \text{где } \alpha_i \geqslant 0, ~x_i \in A, ~i=\overline{1, r+1},~ \sum\limits_{i=1}^{r+1} \alpha_i=1. \end{gather*}
Если $$r \leqslant n$$, то $$x \in B$$. Пусть теперь $$r>n$$. Покажем, что в этом случае $$x$$ можно представить в виде выпуклой комбинации не более чем $$~r~$$ точек множества $$A$$. Если хотя бы одно из чисел $$\alpha_i$$ равно нулю, то это очевидно. Пусть теперь $$\alpha_i>0 ~\forall i$$. Поскольку $$r>n$$, система векторов $$x_i-x_{r+1},~ i=1, \ldots, r$$, линейно зависима. Поэтому найдутся такие числа $$t_1, \ldots, t_r$$, не все равные нулю, что
\begin{gather*} \sum\limits_{i=1}^r t_i\left(x_i-x_{r+1}\right)=0 \end{gather*}
Положим $$t_{r+1}=-\sum\limits_{i=1}^r t_i$$. Тогда $$\sum\limits_{i=1}^{r+1} x_i t_i=0, \sum\limits_{i=1}^{r+1} t_i=0$$ и, значит, для произвольного числа $$c$$ :
\begin{gather}\label{eq1} x=\sum\limits_{i=1}^{r+1} \alpha_i x_i+\sum\limits_{i=1}^{r+1} c t_i x_i=\sum\limits_{i=1}^{r+1}\left(\alpha_i+c t_i\right) x_i, \quad \sum\limits_{i=1}^{r+1}\left(\alpha_i+c t_i\right)=1. \end{gather}
Очевидно, хотя бы одно из чисел $$t_i$$ отрицательно. Кроме того, $$\alpha_i>0$$ для любого $$i$$ и, значит, при $$c=0$$ все числа $$\left(\alpha_i+c t_i\right)$$ положительны. Будем увеличивать параметр $$c$$ от нуля до бесконечности. Тогда, очевидно, существует наименьшее число $$c>0$$ такое, что для всех номеров $$i$$ выполняется $$\left(\alpha_i+c t_i\right) \geqslant 0$$, а для
некоторого $$i_0 \leqslant r+1$$ имеет место $$\left(\alpha_{i_0}+c t_{i_0}\right)=0$$. Поэтому, отбрасывая в представлении (\ref{eq1}) $$i_0$$-е слагаемое $$\left(\alpha_{i_0}+c t_{i_0}\right) x_{i_0}$$, получаем искомое утверждение, т. е. что $$x$$ представимо в виде выпуклой линейной комбинации не более чем $$r$$ точек множества $$A$$.
Повторяя указанную процедуру конечное число раз, получим, что $$r \leqslant n$$ и, значит, $$x \in B$$. Таким образом, доказано, что $$\operatorname{conv} A \subset B$$.
Следствия
Для случая $$n = 1$$ множество $$A\subset \mathbb{R}^1$$ — подмножество прямой, $$\operatorname{conv}(A)$$ — объединение всех отрезков с концами в $$A$$.
Для случая $$n = 2$$ множество $$A \subset \mathbb{R}^2$$ — подмножество координатной плоскости, $$\operatorname{conv}(A)$$ — объединение всех треугольников с вершинами в $$A$$.
Список литературы
1) Арутюнов А. В. "Лекции по выпуклому и многозначному анализу", М.: ФИЗМАТЛИТ, 2004.