Фундаментальная матрица Коши: различия между версиями
Alice1 (обсуждение | вклад) |
Alice1 (обсуждение | вклад) |
||
| Строка 3: | Строка 3: | ||
== Определение == | == Определение == | ||
Фундаментальная матрица Коши $$X(t,\tau)$$ - решение задачи Коши | Фундаментальная матрица Коши $$X(t,\tau)$$ - решение задачи Коши | ||
| − | \ | + | \begin{equation} |
\left\{ | \left\{ | ||
\begin{aligned} | \begin{aligned} | ||
| Строка 10: | Строка 10: | ||
\end{aligned} | \end{aligned} | ||
\right. | \right. | ||
| − | \ | + | \end{equation} |
$$X(t,\tau) = [x^1(t,\tau),\ldots,x^n(t,\tau)]$$, где $$x^j$$ - решение | $$X(t,\tau) = [x^1(t,\tau),\ldots,x^n(t,\tau)]$$, где $$x^j$$ - решение | ||
| Строка 23: | Строка 23: | ||
== Свойства == | == Свойства == | ||
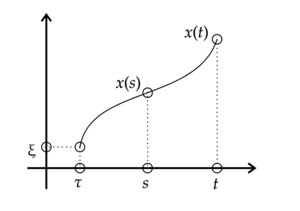
| + | [[Файл:Рис 1.png|мини|справа|Иллюстрация полугруппового свойства.]] | ||
| + | * '''Полугрупповое свойство''': $$X(t,\tau) = X(t,s)X(s,\tau)$$. <br> $$\left\{ \begin{aligned} & \dot x(t)=A(t)x(t),\\ &x(\tau)=\xi. \end{aligned} \right.$$ <br> $$\qquad \Downarrow$$ <br> $$x(t)=X(t,\tau)\xi \Rightarrow \begin{aligned} & x(t) = X(t,s)x(s)\\ & x(s)=X(s,\tau)\xi \end{aligned}$$ | ||
| + | {|style="border-style: solid; border-color: green; background-color:#fefff4; border-width: 1px" | ||
| + | | | ||
| + | $$X(t,\tau)\xi = X(t,s)X(s,\tau)\xi \quad \forall \xi.$$ | ||
| + | |} | ||
| + | |||
| + | ---- | ||
| + | * $$\tau = t$$ <br> $$I=X(t,s)X(s,t)$$ <br> | ||
| + | {|style="border-style: solid; border-color: green; background-color:#fefff4; border-width: 1px" | ||
| + | | | ||
| + | $$X(s,t)=X^{-1}(t,s).$$ | ||
| + | |} | ||
| + | ---- | ||
| + | * Рассмотрим $$I=X(t,\tau)X(\tau,t)$$. <br> Продифференцируем по $$\tau$$: $$0=\frac{\partial X(t,\tau)}{\partial\tau}X(\tau,t)+X(t,\tau)\frac{\partial X(\tau,t)}{\partial\tau}$$. При этом $$\frac{\partial X(\tau,t)}{\partial\tau} = A(\tau)X(\tau,t)$$. <br> Отсюда следует, что | ||
| + | {|style="border-style: solid; border-color: green; background-color:#fefff4; border-width: 1px" | ||
| + | | | ||
| + | $$\frac{\partial X(t,\tau)}{\partial\tau}=-X(t,\tau)A(\tau)$$. | ||
| + | |} | ||
| + | ---- | ||
| + | * $$S(t,\tau)=X^T(\tau,t)$$ <br> $$\frac{\partial S(t,\tau)}{\partial t}=-A^T(t)S(t,\tau)$$ <br> $$\frac{\partial X(\tau,t)}{\partial t}=-X(\tau,t)A(t)$$ <br> $$\Rightarrow $$ | ||
| + | {|style="border-style: solid; border-color: green; background-color:#fefff4; border-width: 1px" | ||
| + | | | ||
| + | $$S(t)=-A^T(t)S(t)$$ - '''сопряжённая система'''. | ||
| + | |} | ||
| + | |||
| + | == Система дифференциальных уравнений с постоянными коэффициентами == | ||
| + | В случае $$A(t) = A = const$$ матрицант равен $$X(t) = e^{A(t-t_0)},$$ где $$e^{As}$$ - матричная экспонента (см. [https://sawiki.cs.msu.ru/index.php?title=%D0%9C%D0%B0%D1%82%D1%80%D0%B8%D1%87%D0%BD%D1%8B%D0%B9_%D1%8D%D0%BA%D1%81%D0%BF%D0%BE%D0%BD%D0%B5%D0%BD%D1%86%D0%B8%D0%B0%D0%BB&action=edit&redlink=1 статью про матричный экспоненциал]), следовательно, матрица Коши: | ||
| + | <br> | ||
| + | $$C(t,s) = e^{A(t-s)},$$ | ||
| + | <br> | ||
| + | $$C(t,s) = X(t-s).$$ | ||
| + | <br> | ||
| + | Таким образом, в этом случае для получения матрицы Коши достаточно подставить $$(t-s)$$ в качестве аргумента матрицанта. | ||
| + | <br> | ||
| + | Общее решение системы линейных неоднородных дифференциальных уравнений с постоянными коэффициентами имеет вид: | ||
| + | \[ | ||
| + | x(t)=e^{A(t-t_0)}x(t_0)+\int\limits_{t_0}^{t}e^{A(t-s)}B(s)ds. | ||
| + | \] | ||
| + | |||
| + | === Пример === | ||
| + | ---- | ||
| + | Рассмотрим систему $$(1)$$ при $$A = \begin{bmatrix} -2 & 12 \\-1 & 5 \end{bmatrix}$$: | ||
| + | <br> | ||
| + | $$ | ||
| + | \left\{ | ||
| + | \begin{aligned} | ||
| + | & \dot x_1(t) = -2x_1(t) + 12 x_2(t),\\ | ||
| + | & \dot x_2(t) = -x_1(t) + 5 x_2(t) + au,\\ | ||
| + | & x_1(0) = x_1^0,\\ | ||
| + | & x_2(0) = x_2^0, | ||
| + | \end{aligned} | ||
| + | \right. | ||
| + | $$ | ||
| + | <br> | ||
| + | где $$u$$ - управление, $$a, x_1^0, x_2^0$$ - некоторые константы. <br> | ||
| + | Найдём матричный экспоненциал. <br> | ||
| + | 1. Найдём собственные значения и собственные векторы матрицы $$A$$. <br> | ||
| + | \[ | ||
| + | \begin{vmatrix} | ||
| + | A - \lambda I | ||
| + | \end{vmatrix} | ||
| + | = | ||
| + | \begin{vmatrix} | ||
| + | -2 -\lambda & 12 \\ -1 & 5-\lambda | ||
| + | \end{vmatrix} | ||
| + | = \lambda^2-3\lambda+2 \Rightarrow \lambda_1=1, \quad \lambda_2=2. | ||
| + | \] | ||
| − | + | При $$\lambda = 1$$ собственный вектор $$(4,1)^T$$. При $$\lambda = 2$$ собственный вектор $$(3,1)^T$$. | |
| − | + | ||
| − | + | 2. Выпишем ФСР. <br> | |
| − | + | $$ x(t) = c_1e^{2t} \begin{bmatrix} 3 \\ 1 \end{bmatrix} + c_2e^t \begin{bmatrix} 4 \\ 1 \end{bmatrix}$$. | |
| + | <br> | ||
| + | Найдём константы $$c_1$$ и $$c_2$$. | ||
| + | <br> | ||
| + | $$\left\{ \begin{aligned} 3c_1+4c_2=1, \\ c_1+c_2=0. \end{aligned} \right. \Rightarrow \left\{ \begin{aligned}& c_1=-1, \\& c_2=1. \end{aligned} \right.$$ | ||
| + | $$\qquad$$ | ||
| + | $$\left\{ \begin{aligned} 3c_1+4c_2=0, \\ c_1+c_2=1. \end{aligned} \right. \Rightarrow \left\{ \begin{aligned}& c_1=4, \\& c_2=-3. \end{aligned} \right.$$ | ||
| + | \[ \text{Тогда } e^{At} = \begin{bmatrix} -3e^{2t}+4e^t & 12e^{2t}-12e^t \\ -e^{2t}+e^t & 4e^{2t}-3e^t \end{bmatrix}. \] | ||
| + | Далее по формуле Коши найдём $$x_1$$ и $$x_2$$: | ||
| + | <br> | ||
| + | $$x(t) = e^{At}x(0) + \int\limits_0^{t} e^{(t-\tau)}B(\tau)d\tau.$$ Здесь $$B = \begin{bmatrix} 0 \\ a \end{bmatrix}.$$ | ||
| + | <br> | ||
| + | Вычислим $$e^{(t-\tau)}B(\tau):$$ $$\begin{bmatrix} a(12e^{2(t-\tau)}-12e^{(t-\tau)}) \\ a(4e^{2(t-\tau)}-3e^{(t-\tau)}) \end{bmatrix}.$$ | ||
| + | <br> | ||
| + | Проинтегрируем $$\int\limits_0^{t} e^{(t-\tau)}B(\tau)d\tau = \begin{bmatrix} 6a \\ a \end{bmatrix}.$$ | ||
| + | <br> | ||
| + | Итого получим | ||
| + | $$ | ||
| + | \begin{aligned} | ||
| + | & x_1 = x_1^0(-3e^{2t}+4e^t) + x_2^0(12e^{2t}-12e^t)+6a,\\ | ||
| + | & x_2 = x_2^0(-e^{2t}+e^t) + x_2^0(4e^{2t}-3e^t)+a. | ||
| + | \end{aligned} | ||
| + | $$ | ||
== Нахождение == | == Нахождение == | ||
Один из возможных способов нахождения фундаментальной матрицы можно найти на вкладке [https://sawiki.cs.msu.ru/index.php/%D0%9F%D1%80%D0%B8%D0%BB%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D1%8F_%D0%BF%D1%80%D0%B5%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F_%D0%9B%D0%B0%D0%BF%D0%BB%D0%B0%D1%81%D0%B0 "Приложение преобразования Лапласа"] | Один из возможных способов нахождения фундаментальной матрицы можно найти на вкладке [https://sawiki.cs.msu.ru/index.php/%D0%9F%D1%80%D0%B8%D0%BB%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D1%8F_%D0%BF%D1%80%D0%B5%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F_%D0%9B%D0%B0%D0%BF%D0%BB%D0%B0%D1%81%D0%B0 "Приложение преобразования Лапласа"] | ||
| + | |||
| + | |||
| + | |||
| + | == Пример применения == | ||
| + | [https://sawiki.cs.msu.ru/index.php?title=%D0%A4%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D0%B0_%D0%9A%D0%BE%D1%88%D0%B8&action=edit&redlink=1 Формула Коши] для траектории линейной системы | ||
| + | \[ | ||
| + | \left\{ | ||
| + | \begin{aligned} | ||
| + | & \dot x(t) = A(t)x(t) + B(t)u(t)+c(t),\\ | ||
| + | & x(t_0)=x^0. | ||
| + | \end{aligned} | ||
| + | \right. | ||
| + | \] | ||
| + | выглядит следующим образом: | ||
| + | \[ | ||
| + | x(t)=X(t,t_0)x^0+\int\limits_{t_0}^{t} X(t,\tau)[B(\tau)u(\tau)+c(\tau)]d\tau. | ||
| + | \] | ||
Версия 00:24, 20 декабря 2020
Фундаментальная матрица системы линейных однородных дифференциальных уравнений - матрица, столбцы которой образуют фундаментальную систему решений этой системы.
Содержание
Определение
Фундаментальная матрица Коши $$X(t,\tau)$$ - решение задачи Коши \begin{equation} \left\{ \begin{aligned} & \frac{\partial X(t,\tau)}{\partial t} = A(t)X(t,\tau),\\ & X(\tau,\tau) = I. \end{aligned} \right. \end{equation}
$$X(t,\tau) = [x^1(t,\tau),\ldots,x^n(t,\tau)]$$, где $$x^j$$ - решение \[ \left\{ \begin{aligned} & \dot x(t) = A(t)x(t),\\ & x(t_0)=x^0. \end{aligned} \right. \]
Свойства
- Полугрупповое свойство: $$X(t,\tau) = X(t,s)X(s,\tau)$$.
$$\left\{ \begin{aligned} & \dot x(t)=A(t)x(t),\\ &x(\tau)=\xi. \end{aligned} \right.$$
$$\qquad \Downarrow$$
$$x(t)=X(t,\tau)\xi \Rightarrow \begin{aligned} & x(t) = X(t,s)x(s)\\ & x(s)=X(s,\tau)\xi \end{aligned}$$
|
$$X(t,\tau)\xi = X(t,s)X(s,\tau)\xi \quad \forall \xi.$$ |
- $$\tau = t$$
$$I=X(t,s)X(s,t)$$
|
$$X(s,t)=X^{-1}(t,s).$$ |
- Рассмотрим $$I=X(t,\tau)X(\tau,t)$$.
Продифференцируем по $$\tau$$: $$0=\frac{\partial X(t,\tau)}{\partial\tau}X(\tau,t)+X(t,\tau)\frac{\partial X(\tau,t)}{\partial\tau}$$. При этом $$\frac{\partial X(\tau,t)}{\partial\tau} = A(\tau)X(\tau,t)$$.
Отсюда следует, что
|
$$\frac{\partial X(t,\tau)}{\partial\tau}=-X(t,\tau)A(\tau)$$. |
- $$S(t,\tau)=X^T(\tau,t)$$
$$\frac{\partial S(t,\tau)}{\partial t}=-A^T(t)S(t,\tau)$$
$$\frac{\partial X(\tau,t)}{\partial t}=-X(\tau,t)A(t)$$
$$\Rightarrow $$
|
$$S(t)=-A^T(t)S(t)$$ - сопряжённая система. |
Система дифференциальных уравнений с постоянными коэффициентами
В случае $$A(t) = A = const$$ матрицант равен $$X(t) = e^{A(t-t_0)},$$ где $$e^{As}$$ - матричная экспонента (см. статью про матричный экспоненциал), следовательно, матрица Коши:
$$C(t,s) = e^{A(t-s)},$$
$$C(t,s) = X(t-s).$$
Таким образом, в этом случае для получения матрицы Коши достаточно подставить $$(t-s)$$ в качестве аргумента матрицанта.
Общее решение системы линейных неоднородных дифференциальных уравнений с постоянными коэффициентами имеет вид:
\[
x(t)=e^{A(t-t_0)}x(t_0)+\int\limits_{t_0}^{t}e^{A(t-s)}B(s)ds.
\]
Пример
Рассмотрим систему $$(1)$$ при $$A = \begin{bmatrix} -2 & 12 \\-1 & 5 \end{bmatrix}$$:
$$
\left\{
\begin{aligned}
& \dot x_1(t) = -2x_1(t) + 12 x_2(t),\\
& \dot x_2(t) = -x_1(t) + 5 x_2(t) + au,\\
& x_1(0) = x_1^0,\\
& x_2(0) = x_2^0,
\end{aligned}
\right.
$$
где $$u$$ - управление, $$a, x_1^0, x_2^0$$ - некоторые константы.
Найдём матричный экспоненциал.
1. Найдём собственные значения и собственные векторы матрицы $$A$$.
\[
\begin{vmatrix}
A - \lambda I
\end{vmatrix}
=
\begin{vmatrix}
-2 -\lambda & 12 \\ -1 & 5-\lambda
\end{vmatrix}
= \lambda^2-3\lambda+2 \Rightarrow \lambda_1=1, \quad \lambda_2=2.
\]
При $$\lambda = 1$$ собственный вектор $$(4,1)^T$$. При $$\lambda = 2$$ собственный вектор $$(3,1)^T$$.
2. Выпишем ФСР.
$$ x(t) = c_1e^{2t} \begin{bmatrix} 3 \\ 1 \end{bmatrix} + c_2e^t \begin{bmatrix} 4 \\ 1 \end{bmatrix}$$.
Найдём константы $$c_1$$ и $$c_2$$.
$$\left\{ \begin{aligned} 3c_1+4c_2=1, \\ c_1+c_2=0. \end{aligned} \right. \Rightarrow \left\{ \begin{aligned}& c_1=-1, \\& c_2=1. \end{aligned} \right.$$
$$\qquad$$
$$\left\{ \begin{aligned} 3c_1+4c_2=0, \\ c_1+c_2=1. \end{aligned} \right. \Rightarrow \left\{ \begin{aligned}& c_1=4, \\& c_2=-3. \end{aligned} \right.$$
\[ \text{Тогда } e^{At} = \begin{bmatrix} -3e^{2t}+4e^t & 12e^{2t}-12e^t \\ -e^{2t}+e^t & 4e^{2t}-3e^t \end{bmatrix}. \]
Далее по формуле Коши найдём $$x_1$$ и $$x_2$$:
$$x(t) = e^{At}x(0) + \int\limits_0^{t} e^{(t-\tau)}B(\tau)d\tau.$$ Здесь $$B = \begin{bmatrix} 0 \\ a \end{bmatrix}.$$
Вычислим $$e^{(t-\tau)}B(\tau):$$ $$\begin{bmatrix} a(12e^{2(t-\tau)}-12e^{(t-\tau)}) \\ a(4e^{2(t-\tau)}-3e^{(t-\tau)}) \end{bmatrix}.$$
Проинтегрируем $$\int\limits_0^{t} e^{(t-\tau)}B(\tau)d\tau = \begin{bmatrix} 6a \\ a \end{bmatrix}.$$
Итого получим
$$
\begin{aligned}
& x_1 = x_1^0(-3e^{2t}+4e^t) + x_2^0(12e^{2t}-12e^t)+6a,\\
& x_2 = x_2^0(-e^{2t}+e^t) + x_2^0(4e^{2t}-3e^t)+a.
\end{aligned}
$$
Нахождение
Один из возможных способов нахождения фундаментальной матрицы можно найти на вкладке "Приложение преобразования Лапласа"
Пример применения
Формула Коши для траектории линейной системы \[ \left\{ \begin{aligned} & \dot x(t) = A(t)x(t) + B(t)u(t)+c(t),\\ & x(t_0)=x^0. \end{aligned} \right. \] выглядит следующим образом: \[ x(t)=X(t,t_0)x^0+\int\limits_{t_0}^{t} X(t,\tau)[B(\tau)u(\tau)+c(\tau)]d\tau. \]