Множество разрешимости линейной управляемой системы, заданной при помощи ОДУ, без помехи. Внешние оценки: различия между версиями
Alexei (обсуждение | вклад) |
Alexei (обсуждение | вклад) |
||
| Строка 54: | Строка 54: | ||
Можно найти в [[Сумма двух эллипсоидов. Внутренние и внешние оценки | статье про внутренние оценки суммы двух эллипсоидов]]. | Можно найти в [[Сумма двух эллипсоидов. Внутренние и внешние оценки | статье про внутренние оценки суммы двух эллипсоидов]]. | ||
| − | + | == Внешняя оценка для суммы эллипсойдов == | |
Обозначим эллипсойд с центром \( q \in \mathcal{R}^n \) и матрицей конфигурации \( Q \in \mathcal{R}^{n \times n}, Q = Q^* > 0\) | Обозначим эллипсойд с центром \( q \in \mathcal{R}^n \) и матрицей конфигурации \( Q \in \mathcal{R}^{n \times n}, Q = Q^* > 0\) | ||
\[ \mathcal{E}(q,Q) = \{x: \langle (x-q), Q^{-1}(x-q) \rangle \leq 1 \} \] | \[ \mathcal{E}(q,Q) = \{x: \langle (x-q), Q^{-1}(x-q) \rangle \leq 1 \} \] | ||
| Строка 66: | Строка 66: | ||
Равенство хдесь достигается тогда и только тогда, когда \( p_i = \sqrt{\langle l,Q_i l \rangle}, i=1,...,n.\). Таким образом опорный вектор по направлению \( l \) совпадает с опорным вектором \( \mathcal{E}_1+ \mathcal{E}_n \), и поэтому | Равенство хдесь достигается тогда и только тогда, когда \( p_i = \sqrt{\langle l,Q_i l \rangle}, i=1,...,n.\). Таким образом опорный вектор по направлению \( l \) совпадает с опорным вектором \( \mathcal{E}_1+ \mathcal{E}_n \), и поэтому | ||
\[\mathcal{E}_1+ \mathcal{E}_n = \bigcup \limits_{l \in S_1} \mathcal{E}_+(l) \] | \[\mathcal{E}_1+ \mathcal{E}_n = \bigcup \limits_{l \in S_1} \mathcal{E}_+(l) \] | ||
| + | |||
== Оценка множества разрешимости == | == Оценка множества разрешимости == | ||
Для системы (\ref{1}) справедлива формула Коши: | Для системы (\ref{1}) справедлива формула Коши: | ||
Версия 14:37, 6 декабря 2022
Внешние оценки множества разрешимости позволяют аппроксимировать это множество "изнутри", а также на основе полученной аппроксимации построить его приближенный вид.
Если вместе со внутренними оценками построить и внешние, то можно точнее оценить, где находится истинное множество разрешимости, т.к. оно располагается между внутренними и внешними оценками.
Будем рассматривать только случай линейной управляемой системы, заданной при помощи ОДУ, без помехи.
Содержание
Постановка задачи
Рассматривается линейная управляемая система дифференциальных уравнений без помехи: \begin{equation} \label{1} \begin{cases} \dot x(t) = A(t)x(t) + B(t)u(t), \\ x(t_0) \in \mathcal{X}_0, \\ u(t) \in \mathcal{P}(t), \end{cases} \end{equation} где \(A(t) \in \mathbb{R}^{n \times n}, \ B(t) \in \mathbb{R}^{n \times m}, \ t \in [t_0, t_1],\) а множества \(\mathcal{X}_0\) и \(\mathcal{P}(t)\) являются эллипсоидами: \[ \mathcal{X}_0 = \mathcal{E}(x_0, X_0) \subset \mathbb{R}^n, \] \[ \mathcal{P}(t) = \mathcal{E}(q(t), Q(t)) \subset \mathbb{R}^m. \] Тут \(x_0 \in \mathbb{R}^n, \ X_0 \in \mathbb{R}^{n\times n}, \ q(t) \in \mathbb{R}^m, \ Q(t) \in \mathbb{R}^{m\times m}\). Построить множество разрешимости.
Эллипсоидные иссчесления
Рассмотрим некотрые необходимые нам свойства эллипсойдных исчислений.
Замечание 1
Т.к. выпуклое множество однозначно определяется своей опорной функцией, то эллипсоид с центром в точке q и матрицей Q можно определить как множество, построенное в направлении некоторого ненулевого вектора l:
\[\mathcal{E}(q, Q) = \{x \in \mathbb{R}^n \:|\: \langle x,\,l \rangle \leq \langle l,\,q \rangle + \langle l,\,Ql \rangle^\frac{1}{2}\},\]
Утверждение 1
Для любой матрицы A и любого эллипсоида с центром в точке q и матрицей Q выполнено тождество:
\[A\mathcal{E}(q,Q) = \mathcal{E}(Aq, AQA').\]
Доказательство
Для доказательства равенства множеств, докажем равенство их опорных функций: \[ \rho(l\:|\:A\mathcal{E}(q,Q)) \stackrel{\text{св-во оп.ф.}}{=} \rho(A'l\:|\:\mathcal{E}(q,Q)) = \langle A'l,\,q \rangle + \sqrt{\langle A'l,\,QA'l \rangle} = \langle l,\,Aq \rangle + \sqrt{\langle l,\,AQA'l \rangle} = \rho(l\:|\:\mathcal{E}(Aq,AQA')). \]
Теорема 1
Для суммы эллипсоидов по Минковскому можно получить внутреннюю эллипсоидальную оценку следующего вида:
\[ \sum\limits^n_{i=1} \mathcal{E}(q_i, Q_i) = \bigcup_{\parallel l \parallel = 1} \mathcal{E}_-(l), \] где \(\mathcal{E}_-(l) = \mathcal{E}(q_i, Q_-)\) — эллипсоид, построенный в направлении \(l\), с центром в \(q_i\) и матрицей \(Q_- = Q'_*Q_*\), где \(Q_* = \sum_{i=1}^n S_i Q_i^\frac{1}{2}\), а \(S_i\) — некоторые ортогональные матрицы.
Доказательство
Можно найти в статье про внутренние оценки суммы двух эллипсоидов.
Внешняя оценка для суммы эллипсойдов
Обозначим эллипсойд с центром \( q \in \mathcal{R}^n \) и матрицей конфигурации \( Q \in \mathcal{R}^{n \times n}, Q = Q^* > 0\) \[ \mathcal{E}(q,Q) = \{x: \langle (x-q), Q^{-1}(x-q) \rangle \leq 1 \} \]
Пусть \( p_1, p_2 ... p_n > 0 \). Покажем, что \[ \mathcal{E}_+ = (p_1 + ... + p_n)(\frac{Q_1}{p_1} + ... + \frac{Q_n}{p_n})\] является внешней оценкой.
Действительно, \[ \rho(l| \mathcal{E}_+) = \sum \limits_{i=1}^n \langle l, Q_i l \rangle + \sum \limits_{i>j} (\dfrac{p_j}{p_i} \langle l, Q_il \rangle +\dfrac{p_i}{p_j} \langle l, Q_jl \rangle) \geq \sum \limits_{i=1}^n \langle l,Q_il \rangle +2 \sum\limits_{i>j} \sqrt{\langle l,Q_il \rangle \langle l,Q_jl \rangle} = \rho (l| \mathcal{E}_1+ \mathcal{E}_n)^2 \] Равенство хдесь достигается тогда и только тогда, когда \( p_i = \sqrt{\langle l,Q_i l \rangle}, i=1,...,n.\). Таким образом опорный вектор по направлению \( l \) совпадает с опорным вектором \( \mathcal{E}_1+ \mathcal{E}_n \), и поэтому \[\mathcal{E}_1+ \mathcal{E}_n = \bigcup \limits_{l \in S_1} \mathcal{E}_+(l) \]
Оценка множества разрешимости
Для системы (\ref{1}) справедлива формула Коши: \[x(t,t_1,x_1) = X(t,t_1)x_1 - \int^{t_1}_t X(t,\tau)B(\tau)u(\tau)d\tau,\]
\medskip \noindent где \(X(t,\tau)\) - фундаментальная матрица, удовлетворяющая системе: \[ \left\{\begin{aligned} & \frac{\partial X(t,\tau)}{\partial t} = A(t)X(t,\tau), \\ & X(\tau,\tau) = I. \end{aligned}\right. \]
\medskip Т.к. множества \(\mathcal{X}_1, \mathcal{P}(t)\)~--- эллипсоиды, то с учетом утверждения 2.3 получим: \[\mathcal{W}[t] = X(t, t_1)\mathcal{X}_1 - \int^{t_1}_t X(t,\tau)B(\tau)\mathcal{P}(\tau)d\tau =\mathcal{E}(X(t,t_1)x_1,\,X(t,t_1)X_1X'(t,t_1)) - \] \[ - \int^{t_1}_t \mathcal{E}(X(t,\tau)B(\tau)q(\tau),\,X(t,\tau)B(\tau)Q(\tau)B'(\tau)X'(t,\tau))d\tau.\]
\medskip Поскольку интеграл в полученном выражении представим как предел интегральных сумм \[\lim_{N \rightarrow \infty} \sum^N_{i=1} \frac{t_1-t}{N} \cdot \mathcal{E}(X(t,\tau_i)B(\tau_i)q(\tau_i),\,X(t,\tau_i)B(\tau_i)Q(\tau_i)B'(\tau_i)X'(t,\tau_i)),\]
Из Теоремы 2.3 можно получить внешнюю оценку: \[\mathcal{E}_+ = \mathcal{E}\left(X(t,t_1)x_1 - \int^{t_1}_t X(t,\tau)B(\tau)q(\tau)d\tau,\,Q_+\right),\] \[Q_+ = \left(p_1-\int^{t_1}_t p(\tau)d\tau\right)\cdot\] \begin{equation} \cdot\left(\frac{X(t,t_1)X_1X'(t,t_1)}{p_1}-\int^{t_1}_t\frac{X(t,\tau)B(\tau)Q(\tau)B'(\tau)X'(t,\tau)}{p(\tau)}d\tau\right), \label{Q_plus} \end{equation}
\medskip \noindent где \(p_1,\,p(\tau)\) определяются выражениями: \begin{equation} p_1 = \langle l(t),\,X(t,t_1)X_1X'(t,t_1)l(t) \rangle^\frac{1}{2}, \label{p1} \end{equation} \begin{equation} p(\tau) = \langle l(t),\, X(t,\tau)B(\tau)Q(\tau)B'(\tau)X'(t,\tau)l(t) \rangle^\frac{1}{2}. \label{ptau} \end{equation}
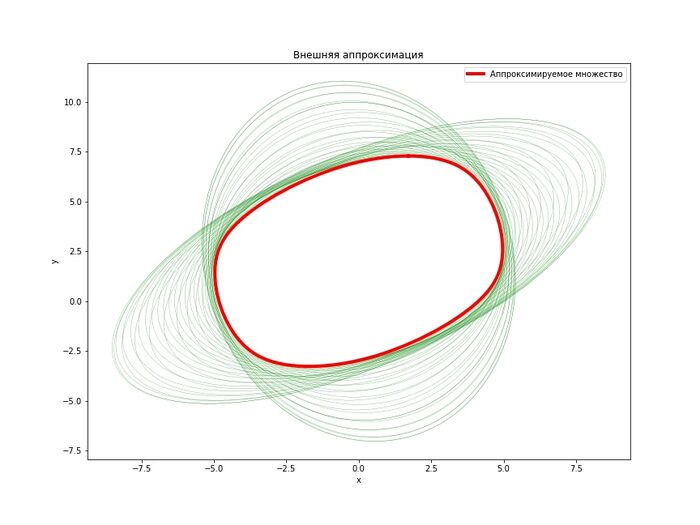
Пример работы программы
\[A(t) = \begin{bmatrix} 1 & t \\ \sin{t} & -1 \end{bmatrix},\;\;B(t) = \begin{bmatrix} -1 & 0.5 \\ t & 10\sin{t} \end{bmatrix},\;\;Q(t) = \begin{bmatrix} 1 & -0.1t^2 \\ -0.1t^2 & 1 \end{bmatrix},\;\;X_1 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},\] \[x_1 = \begin{bmatrix} 20 \\ 0 \end{bmatrix},\;\;q(t) = \begin{bmatrix} 0 \\ 5 \end{bmatrix},\;\;t_1 = 1,\;\;\varepsilon = 10^{-2}.\]