Отображение Пуанкаре. Мешок Бендиксона: различия между версиями
Arthur24 (обсуждение | вклад) |
Arthur24 (обсуждение | вклад) |
||
| Строка 94: | Строка 94: | ||
'''Утверждение 3.''' | '''Утверждение 3.''' | ||
| − | + | Пусть в точке с координатой $$a^*$$ кривая $$\Gamma$$ пересекает предельный цикл $$\gamma$$ системы \eqref{ode} и функция последования $$\psi(\cdot)$$ является дифференцируемой в этой точке. Тогда | |
| + | * если $$|\psi'(a^*)| < 1$$, то предельный цикл $$\gamma$$ — устойчивый; | ||
| + | * если $$|\psi'(a^*)| > 1$$, то предельный цикл $$\gamma$$ — неустойчивый; | ||
| + | * если $$|\psi'(a^*)| = 1$$, то об устойчивости предельного цикла $$\gamma$$ ничего нельзя сказать. | ||
'''Доказательство.''' | '''Доказательство.''' | ||
| − | Следует из [[Циклы в системах с дискретным временем. Теорема Шарковского|теории дискретных динамических систем]]. | + | Следует из [[Циклы в системах с дискретным временем. Теорема Шарковского|теории дискретных динамических систем]] и определения предельного цикла. |
| − | |||
== Список литературы == | == Список литературы == | ||
Версия 13:54, 25 декабря 2024
Мешок Бендиксона
Рассматриваем двумерную динамическую систему \begin{equation}\label{ode} \begin{cases} \dot u_1(t) = f_1(u_1(t),u_2(t)), \\ \dot u_2(t) = f_2(u_1(t),u_2(t)). \end{cases}\quad u\in U\subseteq\mathbb R^2. \end{equation}
Пусть выбрана некоторая траектория $$u(t,u_0)$$ системы \eqref{ode} с начальным условием \begin{equation*} (u_1(0),u_2(0))=(u_1^0,u_2^0)=u_0. \end{equation*}
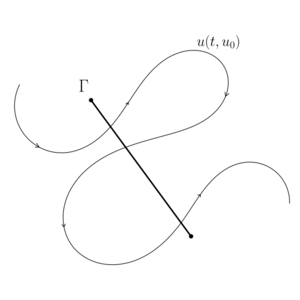
Выберем в координатах $$Ou_1u_2$$ кривую $$\Gamma$$ такую, что
1. $$\Gamma$$ пересекает траекторию $$u(t,u_0)$$ в некоторой точке, обозначим её $$x_1$$;
2. в точках $$\Gamma$$ не происходит касания ни с какой траекторией системы \eqref{ode};
3. по близости с $$\Gamma$$ нет особых точек системы \eqref{ode}.
Отметим, что требование отсутствия по близости к $$\Gamma$$ особых точек наложено из-за случая, когда траектория "разворачивается".
Мы ожидаем, что траектория будет либо спиралевидно "закручиваться" , либо спиралевидно "раскручиваться" , и "развороты" не будут иметь место.
На языке теории векторного поля, это означает, что векторное поле является знакопостоянным в окрестности кривой $$\Gamma$$.
Таким образом, т.к. траектория сама себя не пересекает, внутри области "закручивания" находится предельный цикл или особая точка системы \eqref{ode}. Такому поведению соответствует мешок Бендиксона.
Определение.
Мешком Бендиксона называется область фазового пространства системы \eqref{ode} такая, что указанная траектория $$u(t,u_0)$$ "закручивается" вдоль кривой $$\Gamma$$.
Ограничимся рассмотрением случая, когда система \eqref{ode} имеет предельный цикл $$\gamma$$ внутри мешка Бендиксона.
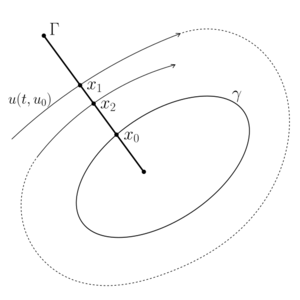
Выберем $$\Gamma$$ — кривая, которая имеет единственную точку пересечения с $$\gamma$$, обозначим её $$x_0$$.
На кривой $$\Gamma$$ введём новую систему координат (одномерную параметризацию). На практике полагают $$\Gamma$$ — отрезок, а система координат соответствует прямой, его содержащей.
По мере эволюции кривая $$u(t,u_0)$$ последовательно пересекает кривую $$\Gamma$$ в точках $$x_1$$, $$x_2$$, $$x_3$$ и т.д. Далее каждой точке $$x_i$$ поставим в соответствие координату $$a_i\in\mathbb{R}$$ в системе координат, отвечающей кривой $$\Gamma$$: \begin{gather*} x_0\mapsto a_0,\quad x_1\mapsto a_1,\quad x_2\mapsto a_2, \quad\dots\quad x_k\mapsto a_k, \quad\dots \end{gather*}
Определение.
Пусть векторное поле, отвечающее \eqref{ode}, знакопостоянно вдоль кривой $$\Gamma$$.
Тогда задана функция последования — числовая функция $$\psi :\mathbb R \mapsto \mathbb R$$, которая определяет, в какой точке произойдет следующее пересечение траектории $$u(t,u_0)$$ с кривой $$\Gamma$$ в системе координат, связанной с $$\Gamma$$:
\begin{gather*}
\psi(a_1)=a_2,\quad\psi(a_2)=a_3,\quad\dots\quad\psi(a_k)=a_{k+1},\quad\dots
\end{gather*}
От исследования предельных циклов \eqref{ode} можно перейти к исследованию замкнутых траекторий \eqref{ode}.
Утверждение 1. Если $$a_0$$ — координата пересечения замкнутой траектории с кривой $$\Gamma$$, то $$\psi(a_0)=a_0$$.
Следовательно, неподвижные точки функции последования $$\psi(\cdot)$$ соответствуют пересечению кривой $$\Gamma$$ с замкнутыми траекториями системы \eqref{ode}.
Отображение Пуанкаре
Отображение Пуанкаре применяется для исследования наличия замкнутых траекторий и устойчивости предельных циклов системы \eqref{ode}. На практике в произвольной области пространства выбирается кривая $$\Gamma$$, отвечающая перечисленным свойствам, с удобной параметризацией, исследуется поведение конкретных траекторий \eqref{ode} внутри окрестности $$\Gamma$$ и нули отображения Пуанкаре.
Введём понятие отображения Пуанкаре. Рассматриваем ту же функцию последования $$\psi(\cdot)$$ из прошлого пункта.
Определение. Отображением Пуанкаре называется числовая функция $$\Pi :\mathbb R \mapsto\mathbb R$$ такая, что \begin{gather*} \Pi(a_1) = \psi(a_1) - \psi(a_2), \\ \Pi(a_2) = \psi(a_2) - \psi(a_3), \\ \dots \\ \Pi(a_k) = \psi(a_k) - \psi(a_{k+1}), \\ \dots \end{gather*}
По определению, неподвижные точки $$\psi(\cdot)$$ соответствуют нулям функции $$\Pi(\cdot)$$ и наоборот.
Утверждение 2.
Чтобы в точке с координатой $$a^*$$ кривая $$\Gamma$$ пересекала замкнутую траекторию системы \eqref{ode}, необходимо и достаточно, чтобы $$\psi(a^*)=a^*$$ или $$\Pi(a^*)=0$$.
Доказательство. Следует из устройства мешка Бендиксона: если положить от противного, что $$\psi(a^*)\neq a^*$$, то траектория либо "закручивается" внутрь себя, либо "раскручивается" от себя, имеем противоречие с замкнутостью данной траектории. В обратную сторону доказываем аналогично.
Утверждение 3.
Пусть в точке с координатой $$a^*$$ кривая $$\Gamma$$ пересекает предельный цикл $$\gamma$$ системы \eqref{ode} и функция последования $$\psi(\cdot)$$ является дифференцируемой в этой точке. Тогда
- если $$|\psi'(a^*)| < 1$$, то предельный цикл $$\gamma$$ — устойчивый;
- если $$|\psi'(a^*)| > 1$$, то предельный цикл $$\gamma$$ — неустойчивый;
- если $$|\psi'(a^*)| = 1$$, то об устойчивости предельного цикла $$\gamma$$ ничего нельзя сказать.
Доказательство. Следует из теории дискретных динамических систем и определения предельного цикла.
Список литературы
1. Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии 2011.
2. Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2024.