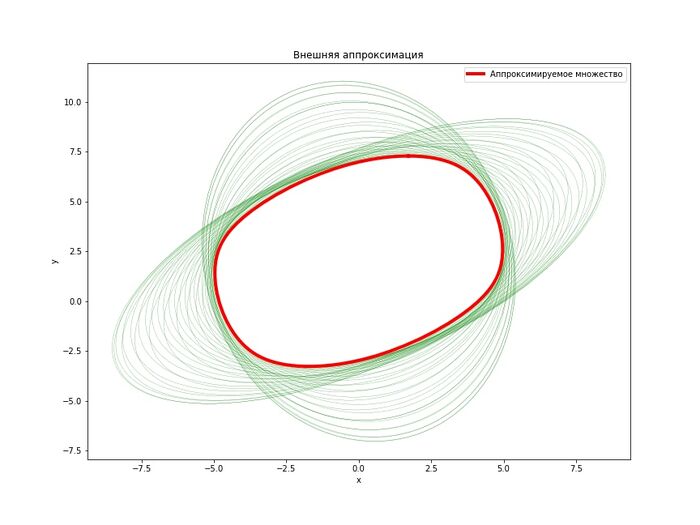
Множество разрешимости линейной управляемой системы, заданной при помощи ОДУ, без помехи. Внешние оценки

Внешние оценки множества разрешимости позволяют аппроксимировать это множество "изнутри", а также на основе полученной аппроксимации построить его приближенный вид.

Если вместе со внутренними оценками построить и внешние, то можно точнее оценить, где находится истинное множество разрешимости, т.к. оно располагается между внутренними и внешними оценками.

Будем рассматривать только случай линейной управляемой системы, заданной при помощи ОДУ, без помехи.

Общий вид системы

Рассматривается линейная управляемая система дифференциальных уравнений без помехи: \begin{equation} \label{1} \begin{cases} \dot x(t) = A(t)x(t) + B(t)u(t), \\ x(t_0) \in \mathcal{X}_0, \\ u(t) \in \mathcal{P}(t), \end{cases} \end{equation} где \(A(t) \in \mathbb{R}^{n \times n}, \ B(t) \in \mathbb{R}^{n \times m}, \ t \in [t_0, t_1],\) а множества \(\mathcal{X}_0\) и \(\mathcal{P}(t)\) являются эллипсоидами: \[ \mathcal{X}_0 = \mathcal{E}(x_0, X_0) \subset \mathbb{R}^n, \] \[ \mathcal{P}(t) = \mathcal{E}(q(t), Q(t)) \subset \mathbb{R}^m. \] Тут \(x_0 \in \mathbb{R}^n, \ X_0 \in \mathbb{R}^{n\times n}, \ q(t) \in \mathbb{R}^m, \ Q(t) \in \mathbb{R}^{m\times m}\).

Некоторые сведения об эллипсоидах

В этом разделе приводятся лишь те некоторые сведения об эллипсоидах, которые требуются в дальнейшем. Более подробную информацию об этих объектах можно получить в основной статье.

Замечание 1

Т.к.  выпуклое множество однозначно определяется своей  опорной функцией, то  эллипсоид с центром в точке q и матрицей Q можно определить как множество, построенное в направлении некоторого ненулевого вектора l:

\[\mathcal{E}(q, Q) = \{x \in \mathbb{R}^n \:|\: \langle x,\,l \rangle \leq \langle l,\,q \rangle + \langle l,\,Ql \rangle^\frac{1}{2}\},\]

Утверждение 1

 Для любой матрицы A и любого эллипсоида с центром в точке q и матрицей Q выполнено тождество:

\[A\mathcal{E}(q,Q) = \mathcal{E}(Aq, AQA').\]

Доказательство

Для доказательства равенства множеств, докажем равенство их опорных функций: \[ \rho(l\:|\:A\mathcal{E}(q,Q)) \stackrel{\text{св-во оп.ф.}}{=} \rho(A'l\:|\:\mathcal{E}(q,Q)) = \langle A'l,\,q \rangle + \sqrt{\langle A'l,\,QA'l \rangle} = \langle l,\,Aq \rangle + \sqrt{\langle l,\,AQA'l \rangle} = \rho(l\:|\:\mathcal{E}(Aq,AQA')). \]

Теорема 1

 Для  суммы эллипсоидов по Минковскому можно получить внутреннюю эллипсоидальную оценку следующего вида:

\[ \sum\limits^n_{i=1} \mathcal{E}(q_i, Q_i) = \bigcup_{\parallel l \parallel = 1} \mathcal{E}_-(l), \] где \(\mathcal{E}_-(l) = \mathcal{E}(q_i, Q_-)\) — эллипсоид, построенный в направлении \(l\), с центром в \(q_i\) и матрицей \(Q_- = Q'_*Q_*\), где \(Q_* = \sum_{i=1}^n S_i Q_i^\frac{1}{2}\), а \(S_i\) — некоторые ортогональные матрицы.

Доказательство

Можно найти в статье про внутренние оценки суммы двух эллипсоидов.

Внешняя оценка для суммы эллипсойдов

Обозначим эллипсойд с центром \( q \in \mathcal{R}^n \) и матрицей конфигурации \( Q \in \mathcal{R}^{n \times n}, Q = Q^* > 0\) \[ \mathcal{E}(q,Q) = \{x: \langle (x-q), Q^{-1}(x-q) \rangle \leq 1 \} \]

Пусть \( p_1, p_2 ... p_n > 0 \). Покажем, что \[ \mathcal{E}_+ = (p_1 + ... + p_n)(\frac{Q_1}{p_1} + ... + \frac{Q_n}{p_n})\] является внешней оценкой.

Действительно, \[ \rho(l| \mathcal{E}_+) = \sum \limits_{i=1}^n \langle l, Q_i l \rangle + \sum \limits_{i>j} (\dfrac{p_j}{p_i} \langle l, Q_il \rangle +\dfrac{p_i}{p_j} \langle l, Q_jl \rangle) \geq \sum \limits_{i=1}^n \langle l,Q_il \rangle +2 \sum\limits_{i>j} \sqrt{\langle l,Q_il \rangle \langle l,Q_jl \rangle} \] = \rho (l| \mathcal{E}_1+ \mathcal{E}_n)^2

Пример работы программы

\[A(t) = \begin{bmatrix} 1 & t \\ \sin{t} & -1 \end{bmatrix},\;\;B(t) = \begin{bmatrix} -1 & 0.5 \\ t & 10\sin{t} \end{bmatrix},\;\;Q(t) = \begin{bmatrix} 1 & -0.1t^2 \\ -0.1t^2 & 1 \end{bmatrix},\;\;X_1 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},\] \[x_1 = \begin{bmatrix} 20 \\ 0 \end{bmatrix},\;\;q(t) = \begin{bmatrix} 0 \\ 5 \end{bmatrix},\;\;t_1 = 1,\;\;\varepsilon = 10^{-2}.\]