Теорема Брауэра

Будем рассматривать конечномерное евклидово пространство \(E\) с нормой \(||\cdot||_E\) и некоторое множество \(M \subset E\). Под сходимостью в пространстве \(E\) будем понимать сходимость по заданной норме.

Формулировка

Любое непрерывное отображение выпуклого компактного множества в себя имеет неподвижную точку, то есть для любого выпуклого компакта \(M\) и непрерывного отображения \(f: M \rightarrow M\) существует \(x^* \in M: f(x^*) = x^*\).

Доказательство

Достаточно доказать эту теорему для единичного шара \(B = \{ x \in E: ||x||_E \leqslant 1\}\subset E\) и соответствующего непрерывного отображения \(f: B \rightarrow B\).

Для начала сформулируем важное топологическое утверждение.

Утверждение. Единичная сфера \(S = \{ x \in E: ||x||_E = 1\}\) не является ретрактом единичного шара \(B\), то есть не существует непрерывного отображения \(\xi: B \rightarrow S\) такого, что \(\xi(x) = x\) для любого \(x \in S\).

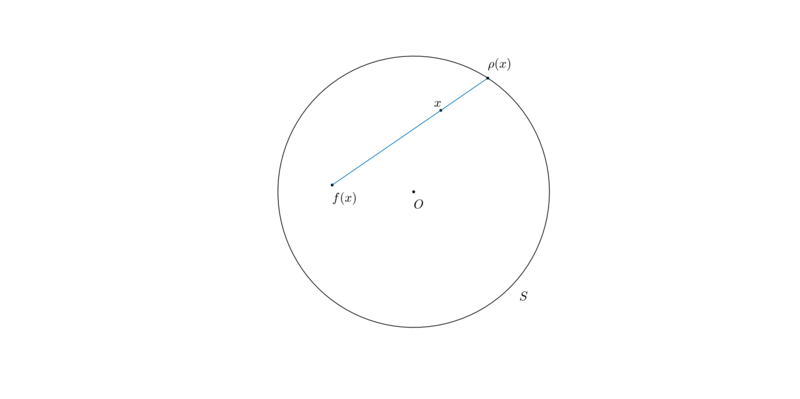
Доказательство этого утверждения можно найти в [1]. Положим, что у отображения \(f: B \rightarrow B\) нет неподвижных точек. Тогда через любую точку \(x \in B\) и её образ \(f(x) \in B\) можно провести прямую, которая пересекает сферу \(S\). Пусть отображение \(\rho: B \rightarrow S\) ставит в соответствие каждой точке шара точку пересечения луча с началом в точке \(f(x)\), проходящего через точку \(x\), и сферы \(S\). Тогда по построению каждой точке шара \(x \in B\) соответствует единственная точка сферы \(\rho(x) \in S\), а также справедливо \(\rho(x) = x\) для \(\forall x \in S\).

Докажем непрерывность этого отображения в шаре: рассмотрим произвольную точку \(x \in B\) и последовательность \(\{ x_n \}_{n=0}^{\infty} \subset B\), cходящуюся к \(x\). Обозначим \(y = \rho(x)\) и рассмотрим последовательность \(\{ y_n = \rho(x_n) \}_{n=0}^{\infty} \subset S\). Единичная сфера \(S\) является компактным множеством, поэтому из последовательности \(\{ y_n\}_{n=0}^{\infty}\) можно выделить сходящуюся подпоследовательность \(\{ y_{n_k} \}_{k=0}^{\infty}\), положим она сходится к \(\overline{y} \in S\). Если \(y \not= \overline{y}\), то, переходя к подпоследовательностям, получаем противоречие \(y = \rho(x) = \lim\limits_{k \rightarrow \infty} \rho(x_{n_k}) = \overline{y}\). Получается, что любая сходящаяся подпоследовательность \(\{ y_{n_k} \}_{k = 0}^{\infty}\) сходится к \(y\), а, следовательно, сама последовательность \(\{ y_n\}_{n=0}^{\infty}\) сходится к \(y\). Итого имеем, что для любой \(\{x_n\}_{n=0}^{\infty} \subset B: x_n \overset{n \rightarrow \infty}{\longrightarrow} x\) справедливо \(\rho(x_n) \overset{n \rightarrow \infty}{\longrightarrow} \rho(x)\), что и означает непрерывность отображения \(\rho\).

Таким образом, при предположении о том, что у \(f\) нет неподвижных точек, было построено непрерывное отображение \(\rho: B \rightarrow S\), для которого справедливо \(\rho(x) = x\) для \(\forall x \in S\), которое не может существовать по вышеописанному утверждению. Следовательно, предположение неверно и \(f\) имеет хотя бы одну неподвижную точку в шаре \(B\).

Особенности

• Выпуклость области определения отображения не является строго необходимой. Теорема справедлива для любого множества, гомеоморфного замкнутому шару, что справедливо для любого выпуклого компакта в \(E\). Формальное обобщение теоремы Брауэра о неподвижной точке без требования выпуклости области определения рассматриваемого отображения может быть получено из теоремы Лефшеца о неподвижной точке.

• Отображение \(f\) не обязано быть сюръективным, то есть образ области определения отображения \(f(M)\) не обязан совпадать с \(M\). Достаточно включения \(f(M) \subseteq M\), и теорема справедлива для отображения с «суженной» областью значений \(\hat{f}: M \rightarrow f(M)\).

• Теорема Брауэра даёт результат лишь о существовании неподвижной точки, но не о единственности. Например, тождественное отображение шара в себя удовлетворяет условиям теоремы, и множеством его неподвижных точек является весь шар.

Существенность условий теоремы

Покажем, что каждое из условий теоремы существенно, то есть при нарушении хотя бы одного из них неподвижная точка может не существовать.

• Отображение как эндоморфизм, то есть область определения и область значений отображения должны совпадать. Пусть \(M = \left[ 0, 1\right]\) и \(f: \left[ 0, 1\right] \rightarrow \left[ 1, 2\right]\), \(f(x) = x + 1\). \(M\) является выпуклым компактом, и \(f\) непрерывно, но не является эндоморфизмом. Нетрудно видеть, что у данного отображения нет неподвижных точек.

• Непрерывность отображения. Положим \(M = \left[ -\frac{1}{2}, \frac{1}{2}\right]\) и рассмотрим отображение

\begin{equation*} f(x) = \begin{cases} \begin{aligned} &\frac{1}{2}, &x = 0, \\ &x^2, &x \not= 0. \end{aligned} \end{cases} \end{equation*} \(M\) выпукло и компактно, однако отображение \(f\) не является непрерывным. Как видно из построения, у \(f\) нет неподвижных точек.

• Выпуклость области определения. Возьмём произвольное \(\varepsilon \in (0, 1)\) и положим \(M = \left[ -1, -\varepsilon\right] \cup \left[ \varepsilon, 1\right]\), \(f(x) = \frac{1}{2} x\). Отображение \(f\) непрерывно, и множество \(M\) компактно, но не выпукло. Нетрудно заметить, что единственная возможная неподвижная точка \(x^* = 0\) не принадлежит \(M\).

• Компактность области определения. Положим \(M = \left( -1, 1\right)\) и \(f(x) = \frac{1}{2}(x + 1)\). Отображение \(f\) непрерывно, и множество \(M\) выпукло, но не компактно. Нетрудно заметить, что единственная возможная неподвижная точка \(x^* = 1\) не принадлежит \(M\).

Литература

1. Борисович Ю.Г., Близняков Н.М., Израилевич Я.А., Фоменко Т.Н. Введение в топологию. — М: Наука, 1995.