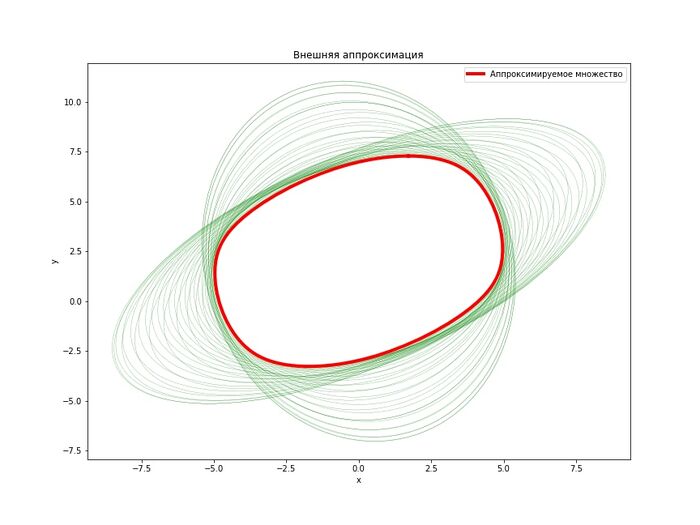
Множество разрешимости линейной управляемой системы, заданной при помощи ОДУ, без помехи. Внешние оценки

Внешние оценки множества разрешимости позволяют аппроксимировать это множество "снаружи", а также на основе полученной аппроксимации построить его приближенный вид. Также существуют внутренние оценки которые позволяют аппроксимировать множество "изнутри".

Постановка задачи

Рассматривается линейная управляемая система дифференциальных уравнений без помехи: \begin{equation} \label{1} \begin{cases} \dot x(t) = A(t)x(t) + B(t)u(t), \\ x(t_1) \in \mathcal{X}_1, \\ u(t) \in \mathcal{P}(t), \end{cases} \end{equation} где \(A(t) \in \mathbb{R}^{n \times n}, \ B(t) \in \mathbb{R}^{n \times m}, \ t \in [t_0, t_1],\) а множества \(\mathcal{X}_1\) и \(\mathcal{P}(t)\) являются эллипсоидами: \[ \mathcal{X}_1 = \mathcal{E}(x_1, X_1) \subset \mathbb{R}^n, \] \[ \mathcal{P}(t) = \mathcal{E}(q(t), Q(t)) \subset \mathbb{R}^m. \] Тут \(x_0 \in \mathbb{R}^n, \ X_1 \in \mathbb{R}^{n\times n}, \ q(t) \in \mathbb{R}^m, \ Q(t) \in \mathbb{R}^{m\times m}\). Матрицы \(A(t), B(t), q(t), Q(t) \) - непрерывны на \([t_0, t_1] \)

Задача состоит в построение множества разрешимости для нашей системы.

Эллипсоидные свойства

Рассмотрим некоторые необходимые нам свойства эллипсоидного исчисления.

Замечание 1

Т.к.  выпуклое множество однозначно определяется своей  опорной функцией, то  эллипсоид с центром в точке q и матрицей Q можно определить как множество, построенное в направлении некоторого ненулевого вектора l:

\[\mathcal{E}(q, Q) = \{x \in \mathbb{R}^n \:|\: \forall l \: \langle x,\,l \rangle \leq \langle l,\,q \rangle + \langle l,\,Ql \rangle^\frac{1}{2}\},\]

Утверждение 1

 Для любой матрицы A и любого эллипсоида с центром в точке q и матрицей Q выполнено тождество:

\[A\mathcal{E}(q,Q) = \mathcal{E}(Aq, AQA').\]

Доказательство

Для доказательства равенства множеств, докажем равенство их опорных функций: \[ \rho(l\:|\:A\mathcal{E}(q,Q)) \stackrel{\text{св-во оп.ф.}}{=} \rho(A'l\:|\:\mathcal{E}(q,Q)) = \langle A'l,\,q \rangle + \sqrt{\langle A'l,\,QA'l \rangle} = \langle l,\,Aq \rangle + \sqrt{\langle l,\,AQA'l \rangle} = \rho(l\:|\:\mathcal{E}(Aq,AQA')). \]

Внешняя оценка для суммы эллипсоидов

Обозначим эллипсоид с центром \( q \in \mathbb{R}^n \) и матрицей конфигурации \( Q \in \mathbb{R}^{n \times n}\) \[ \mathcal{E}(q,Q) = \{x: \langle (x-q), Q^{-1}(x-q) \rangle \leq 1 \} \]

Построим внешнюю оценку для \[ \sum \limits_{i=1}^m \mathcal{E}_i \] где \[ \mathcal{E}_i = \mathcal{E} (p_i, Q_i), p_i > 0\] Рассмотрим эллипсоид \( \mathcal{E}_+(q_+, Q_+) \), где \[ \mathcal{Q}_+ = \left(p_1 + ... + p_m \right) \left(\frac{Q_1}{p_1} + ... + \frac{Q_m}{p_m} \right)\] \[p_+ = \sum \limits_{i=1}^m p_i\]

Действительно, \[ \rho(l| \mathcal{E}_+) = \langle \sum \limits_{i=1}^m q_i, l \rangle + \sqrt{\sum \limits_{i=1}^m \langle l, Q_i l \rangle + \sum \limits_{i=1}^m \sum \limits_{j=1, \\ j \neq i}^m (\dfrac{p_j}{p_i} \langle l, Q_il \rangle )} \geq \left \{ \dfrac{a+b}{2} \geq \sqrt{ab} \right \} \geq \langle \sum \limits_{i=1}^m q_i, l \rangle + \sqrt{\sum \limits_{i=1}^m \langle l,Q_il \rangle +2 \sum\limits_{i>j} \sqrt {\langle l,Q_il \rangle \langle l,Q_jl \rangle}} = \rho (l| \mathcal{E}_1+...+\mathcal{E}_m) \] Отсюда следует \[ \sum \limits^m_{i=1} \mathcal{E}(q_i,Q_i) \subseteq \mathcal{E}_+ \] Равенство здесь достигается при условии равенства \( \dfrac{a+b}{2} = \sqrt{ab}\) что в свою очередь происходит тогда и только тогда, когда \( p_i = \sqrt{\langle l,Q_i l \rangle}, i=1,...,m.\).

Оценка множества разрешимости

Для системы (\ref{1}) справедлива формула Коши: \[x(t,t_1,x_1) = X(t,t_1)x_1 - \int^{t_1}_t X(t,\tau)B(\tau)u(\tau)d\tau,\] где \(X(t, \tau) \) - фундаментальная матрица,удовлетворяющая системе:

\[ \left\{\begin{aligned} & \frac{\partial X(t,\tau)}{\partial t} = A(t)X(t,\tau), \\ & X(\tau,\tau) = I. \end{aligned}\right. \]

Т.к. множества \(\mathcal{X}_1, \mathcal{P}(t)\) эллипсоиды, то с учетом утверждения 1 получим: \[\mathcal{W}[t] = X(t, t_1)\mathcal{X}_1 - \int^{t_1}_t X(t,\tau)B(\tau)\mathcal{P}(\tau)d\tau =\mathcal{E}(X(t,t_1)x_1,\,X(t,t_1)X_1X'(t,t_1)) - \] \[ - \int^{t_1}_t \mathcal{E}(X(t,\tau)B(\tau)q(\tau),\,X(t,\tau)B(\tau)Q(\tau)B'(\tau)X'(t,\tau))d\tau.\]

Разобьем отрезок \( [t,t_1] \) на N частей, так чтобы i -ый отрезок имел вид \( [t + (i-1) \dfrac{t_1 - t}{N}, t + i \dfrac{t_1 - t}{N}] \). Тогда интегральная сумма примет вид \[\lim_{N \rightarrow \infty} \sum^N_{i=1} \frac{t_1-t}{N} \cdot \mathcal{E}(X(t,\tau_i)B(\tau_i)q(\tau_i),\,X(t,\tau_i)B(\tau_i)Q(\tau_i)B'(\tau_i)X'(t,\tau_i)),\]

Из внешней оценки для суммы эллипсоидов можно получить внешнюю оценку: \begin{equation} \mathcal{E}_+ = \mathcal{E}\left(X(t,t_1)x_1 - \int^{t_1}_t X(t,\tau)B(\tau)q(\tau)d\tau,\,Q_+\right),\\ Q_+ = \left(p_1-\int^{t_1}_t p(\tau)d\tau\right)\cdot \left(\frac{X(t,t_1)X_1X'(t,t_1)}{p_1}-\int^{t_1}_t\frac{X(t,\tau)B(\tau)Q(\tau)B'(\tau)X'(t,\tau)}{p(\tau)}d\tau\right), \label{Q_plus} \end{equation}

где \(p_1,\,p(\tau)\) определяются выражениями: \begin{equation} p_1 = \langle l(t),\,X(t,t_1)X_1X'(t,t_1)l(t) \rangle^\frac{1}{2}, \label{p1} \end{equation} \begin{equation} p(\tau) = \langle l(t),\, X(t,\tau)B(\tau)Q(\tau)B'(\tau)X'(t,\tau)l(t) \rangle^\frac{1}{2}. \label{ptau} \end{equation}

Оптимизация вычислений внешней оценки

Из выражений (\ref{1})-(\ref{ptau}) следует, что матрица эллипсоида внешней оценки в направлении \(l\) определяется формулами: \[Q_+ = \left(p_1-\int^{t_1}_t p(\tau)d\tau\right)\left(\frac{X(t,t_1)X_1X'(t,t_1)}{p_1}-\int^{t_1}_t\frac{X(t,\tau)B(\tau)Q(\tau)B'(\tau)X'(t,\tau)}{p(\tau)}d\tau\right),\] \[p_1 = \langle l(t),\,X(t,t_1)X_1X'(t,t_1)l(t) \rangle^\frac{1}{2},\] \[p(\tau) = \langle l(t),\, X(t,\tau)B(\tau)Q(\tau)B'(\tau)X'(t,\tau)l(t) \rangle^\frac{1}{2}.\]

Здесь \(p_1, p(\tau)\) так же зависят от \(t\). Cделаем замену: \[l(t) = X'(t_1,t)l_1.\]

Тогда выражения для \(p_1, p(\tau)\) преобразуются: \[p_1 = \langle l_1,\,X_1l_1 \rangle^\frac{1}{2},\] \[p(\tau) = \langle l_1,\,X(t_1,\tau)B(\tau)Q(\tau) B'(\tau)X'(t_1,\tau)l_1 \rangle^\frac{1}{2}.\]

Построение внешней оценки

Обозначим: \[\tilde{A}(t) = p_1 - \int^{t_1}_t p(\tau)d\tau,\] \[\tilde{B}(t) = \frac{X(t,t_1)X_1X'(t,t_1)}{p_1} - \int^{t_1}_t\frac{X(t,\tau)B(\tau)Q(\tau)B'(\tau)X'(t,\tau)}{p(\tau)}d\tau.\]

Тогда (\ref{Q_plus}) преобразуется в: \[Q_+(t) = \tilde{A}(t)\tilde{B}(t).\]

Продифференцируем полученное выражение: \[\dfrac{\partial Q_+(t)}{\partial t} = \dfrac{\partial \tilde{A}}{\partial t}\tilde{B} + \tilde{A}\frac{\partial \tilde{B}}{\partial t} = p(t)\tilde{B}(t) +\] \[+ \tilde{A}\left( \dfrac{A(t)X(t,\tau)X_1X'(t,\tau) + X(t,\tau)X_1X'(t,\tau)A'(t)}{p_1} + \dfrac{B(t)Q(t)B'(t)}{p(t)} \right) -\] \[-\tilde{A}\int^{t_1}_t \dfrac{A(t)X(t,\tau)B(\tau)Q(\tau)B'(\tau)X'(t,\tau) + X(t,\tau)B(\tau)Q(\tau)B'(\tau)X'(t,\tau)A'(t)}{p(\tau)}d\tau = \] \[= p(t)\tilde{B}(t) + \tilde{A(t)}\left( A(t)\tilde{B}(t) + \tilde{B}(t)A'(t) + \dfrac{B(t)Q(t)B'(t)}{p(t)} \right) = \{\tilde{A}(t) \in \mathbb{R}^{1\times 1}\} =\] \[= p(t)\tilde{B}(t) + A(t)\tilde{A}(t)\tilde{B}(t) + \tilde{A}(t)\tilde{B}(t)A'(t) + \tilde{A}(t)\dfrac{B(t)Q(t)B'(t)}{p(t)} = \] \[= p(t)\tilde{B}(t) + A(t)Q_+(t) + Q_+(t)A'(t) + \tilde{A}(t)\dfrac{B(t)Q(t)B'(t)}{p(t)}.\]

Таким образом, получим: \begin{equation} \begin{cases} & \dfrac{\partial Q_+(t)}{\partial t} = p(t)\tilde{B}(t) + A(t)Q_+(t) + Q_+(t)A'(t) + \tilde{A}(t)\dfrac{B(t)Q(t)B'(t)}{p(t)}, \\ & Q_+(t_1) = X_1. \label{u3} \end{cases} \end{equation}

При этом для \(\tilde{A}(t), \tilde{B}(t)\) можно также выразить систему дифференциальных уравнений: \begin{equation} \begin{cases} \dfrac{\partial \tilde{A}(t)}{\partial t} = p(t), \\ \dfrac{\partial \tilde{B}(t)}{\partial t} = A(t)\tilde{B}(t) + \tilde{B}(t)A'(t) + \dfrac{B(t)Q(t)B'(t)}{p(t)}, \\ \tilde{A}(t_1) = p_1, \\ \tilde{B}(t_1) = \dfrac{X_1}{p_1}. \label{u2} \end{cases} \end{equation}

Вспомним, что фундаментальная матрица \(X(t,t_1)\) определяется следующей системой: \begin{equation} \begin{cases} \label{u1} \dfrac{\partial X(t,\tau)}{\partial t} = A(t)X(t,\tau), \\ X(\tau,\tau) = I. \end{cases} \end{equation}

Совместно решая системы (\ref{u3}), (\ref{u2}) и (\ref{u1}), можно получить \(Q_+(t)\) численным интегрированием. Центр искомого эллипсоида также удовлетворяет системе (\ref{q_sys}):

\begin{equation} \begin{cases} \dfrac{\partial q_\varepsilon}{\partial t} = A(t)q_\varepsilon(t) + B(t)q_\varepsilon(t), \\ q_\varepsilon(t_1) = x_1. \label{q_sys} \end{cases} \end{equation}

Пример вычисленния

Приведем примеры численных вычислений с помощью внешних оценок для наглядности наших аналитических вычислений. Данный алгоритм выходит за рамки нашей статьи, так что мы не будем рассматривать их. Однако для пытливых слушателей приведу разделы необходимые знать для реализации численных вычислений:

• гиперсферической системой координат
• Численное дифференцирование
• Численное интегрирование
• Описание функции Mathalab ode45

\[A(t) = \begin{bmatrix} 1 & t \\ \sin{t} & -1 \end{bmatrix},\;\;B(t) = \begin{bmatrix} -1 & 0.5 \\ t & 5\sin{t} \end{bmatrix},\;\;Q(t) = \begin{bmatrix} 2 & -0.3t^2 \\ -0.2t^2 & 1 \end{bmatrix},\;\;X_1 = \begin{bmatrix} 2 & 0 \\ 0 & 3 \end{bmatrix},\] \[x_1 = \begin{bmatrix} 20 \\ 0 \end{bmatrix},\;\;q(t) = \begin{bmatrix} 0 \\ 5 \end{bmatrix},\;\;t_1 = 1,\;\;\varepsilon = 10^{-3}.\]

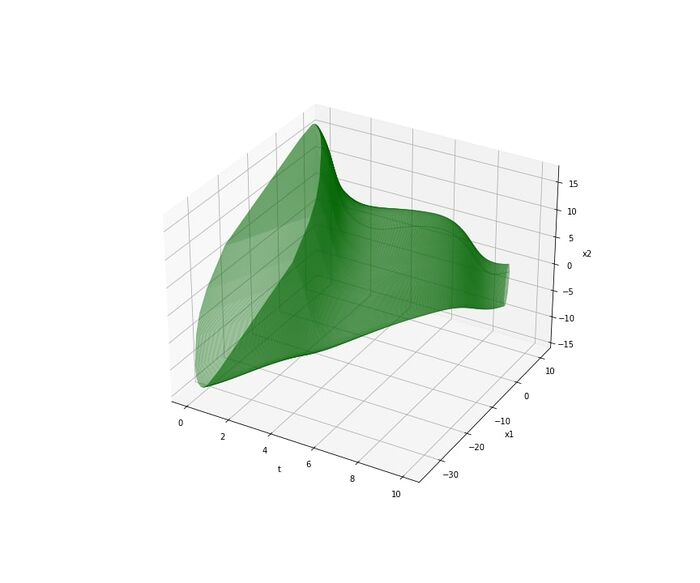
Трубка разрешимости для указанной системы будет иметь вид: