Модель динамики популяции жуков (Tribolium): различия между версиями
Margo23 (обсуждение | вклад) |
Margo23 (обсуждение | вклад) |
||
| Строка 37: | Строка 37: | ||
т.к. система линейна, получим единственную неподвижную точку — $$M(0,0, 0)$$ — неустойчива, при $$b > 1$$. | т.к. система линейна, получим единственную неподвижную точку — $$M(0,0, 0)$$ — неустойчива, при $$b > 1$$. | ||
| − | + | == Биффуркационная диаграмма == | |
| − | Для относительно низких коэффициентов смертности численность личинок приходит в стационарное состояние (неподвижную точку). При $$\nu_A > 0.1$$ существует устойчивый цикл периода два, когда численность личинок колеблется между двумя существенно различными величинами - "вспышки численности". При $$\nu_A > 0.6$$ цикл исчезает, остается единственная устойчивая неподвижная точка. Для высоких значений коэффициента смертности решение имеет сложное непериодическое поведение. | + | Рассмотрим схематическое изображение [https://sawiki.cs.msu.ru/index.php/%D0%91%D0%B8%D1%84%D1%83%D1%80%D0%BA%D0%B0%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D0%B0%D1%8F_%D0%B4%D0%B8%D0%B0%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B0 бифуркационной диаграммы] модели. Бифуркационный параметр — коэффициент смертности взрослых особей. [[Файл:Бифжук.jpg|мини|Схематическое изображение бифуркационной диаграммы модели (1).]] |
| + | * Для относительно низких коэффициентов смертности численность личинок приходит в стационарное состояние (неподвижную точку). | ||
| + | * При $$\nu_A > 0.1$$ существует [https://sawiki.cs.msu.ru/index.php/%D0%A6%D0%B8%D0%BA%D0%BB%D1%8B_%D0%B2_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0%D1%85_%D1%81_%D0%B4%D0%B8%D1%81%D0%BA%D1%80%D0%B5%D1%82%D0%BD%D1%8B%D0%BC_%D0%B2%D1%80%D0%B5%D0%BC%D0%B5%D0%BD%D0%B5%D0%BC._%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%A8%D0%B0%D1%80%D0%BA%D0%BE%D0%B2%D1%81%D0%BA%D0%BE%D0%B3%D0%BE устойчивый цикл] периода два, когда численность личинок колеблется между двумя существенно различными величинами - "вспышки численности". | ||
| + | * При $$\nu_A > 0.6$$ цикл исчезает, остается единственная устойчивая неподвижная точка. | ||
| + | * Для высоких значений коэффициента смертности решение имеет сложное непериодическое поведение. | ||
== Улучшение модели == | == Улучшение модели == | ||
| Строка 59: | Строка 63: | ||
$$~C_{ap}$$ - количество куколок съеденных взрослыми особями. | $$~C_{ap}$$ - количество куколок съеденных взрослыми особями. | ||
| + | |||
| + | ==Список литературы== | ||
| + | |||
| + | 1. Братусь А. С., Новожилов А. С., Платонов А. П. Динамические системы и модели биологии 2011. | ||
| + | |||
| + | 2. Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023. | ||
Версия 17:20, 30 октября 2023
Содержание
Базовая модель динамики жуков
Математические модели биоматематики нередко рассматриваются с целью понимания неких экономических эффектов и управления ими. Так, группа исследователей предложила модель популяции мучного жука Tribolium.
Жук Tribolium имеет три стадии развития: личинки - larva (L), куколки - pupa (P) и взрослая особь - adult (A). Динамическая модель численности жука, в которой естественно принять за единицу времени две недели, имеет вид: \begin{gather*} L \qquad P \qquad A \end{gather*}
\begin{equation} \label{sys1} \begin{cases} L_{t+1} = bA_t,\\ P_{t+1} = (1-\nu_L)L_t,\\ A_{t+1} = (1-\nu_P)P_t+(1+\nu_A)A_t, \end{cases} \end{equation} где $$\nu_{(\cdot)}$$ - отношение количества погибающих естественным путем особей соответствующего вида к их общему числу, $$b -$$ коэффициент рождаемости (количество личинок, отложенных одним взрослым насекомым за единицу времени).
Исследование динамической системы
Исследуем неподвижные точки системы $$\ref{(sys1)}$$ рассмотрев её матрицу якоби: \[ \begin{cases} L = bA,\\ P = (1-\nu_L)L,\\ A = (1-\nu_P)P +(1+\nu_A)A, \end{cases} \quad \Rightarrow \quad J = \left( \begin{array}{ccccc} 0 & 0 & b \\ 1 - \nu_L & 0 & 0 \\ 0 & 1-\nu_P & 1-\nu_A\\ \end{array} \right), \] т.к. система линейна, получим единственную неподвижную точку — $$M(0,0, 0)$$ — неустойчива, при $$b > 1$$.
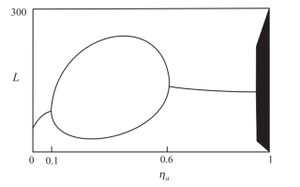
Биффуркационная диаграмма
Рассмотрим схематическое изображение бифуркационной диаграммы модели. Бифуркационный параметр — коэффициент смертности взрослых особей.
- Для относительно низких коэффициентов смертности численность личинок приходит в стационарное состояние (неподвижную точку).
- При $$\nu_A > 0.1$$ существует устойчивый цикл периода два, когда численность личинок колеблется между двумя существенно различными величинами - "вспышки численности".
- При $$\nu_A > 0.6$$ цикл исчезает, остается единственная устойчивая неподвижная точка.
- Для высоких значений коэффициента смертности решение имеет сложное непериодическое поведение.
Улучшение модели
В реальности динамика популяции жука Tribolium имеет особенность. Когда популяция жуков достигает некоторой плотности, взрослые особи начинают поедать куколок и отложенные яйца (будущие личинки), сами личинки также поедают яйца. С учетом этих обстоятельств исходная модель приобретает вид:
\begin{equation} \label{sys2} \begin{cases} L_{t+1} = bA_te^{-C_{ll}A_t - C_{al}L_t},\\ P_{t+1} = (1-\nu_L)L_t,\\ A_{t+1} = (1-\nu_P)P_te^{-C_{pa}A_t}+(1+\nu_A)A_t, \end{cases} \end{equation}
Обозначения:
$$~C_{al}$$ - количество личинок съеденных взрослыми особями.
$$~C_{ll}$$ - коэффициент каннибализма личинок.
$$~C_{ap}$$ - количество куколок съеденных взрослыми особями.
Список литературы
1. Братусь А. С., Новожилов А. С., Платонов А. П. Динамические системы и модели биологии 2011.
2. Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023.