Модель динамики популяции жуков (Tribolium): различия между версиями
Margo23 (обсуждение | вклад) |
Margo23 (обсуждение | вклад) |
||
| Строка 16: | Строка 16: | ||
== Исследование динамической системы == | == Исследование динамической системы == | ||
'''Определение 1'''. | '''Определение 1'''. | ||
| − | Неподвижная точка системы $u_{t+1}=f(u_t)$ — это такая точка $$ N^* \in \mathbb{R} $$, что $$ f(N^*)=N^* $$. | + | Неподвижная точка системы $$ u_{t+1}=f(u_t) $$ — это такая точка $$ N^* \in \mathbb{R} $$, что $$ f(N^*)=N^* $$. |
Исследуем [https://sawiki.cs.msu.ru/index.php/%D0%9D%D0%B5%D0%BF%D0%BE%D0%B4%D0%B2%D0%B8%D0%B6%D0%BD%D1%8B%D0%B5_%D1%82%D0%BE%D1%87%D0%BA%D0%B8_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B неподвижные точки] системы (1) по определению: | Исследуем [https://sawiki.cs.msu.ru/index.php/%D0%9D%D0%B5%D0%BF%D0%BE%D0%B4%D0%B2%D0%B8%D0%B6%D0%BD%D1%8B%D0%B5_%D1%82%D0%BE%D1%87%D0%BA%D0%B8_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B неподвижные точки] системы (1) по определению: | ||
| Строка 29: | Строка 29: | ||
\Rightarrow | \Rightarrow | ||
\quad | \quad | ||
| − | J = | + | J = \begin{cases} |
| − | \begin{ | + | L = bA,\\ |
| − | + | P = (1-\nu_L)bA,\\ | |
| − | 1 - \nu_L | + | A = (1-\nu_P)(1-\nu_L)bA +(1+\nu_A)A, |
| − | + | \end{cases}, | |
| − | \ | + | \] |
| − | \ | + | \[ |
| + | b = -\dfrac{(1+\nu_A)}{(1-\nu_P)(1-\nu_L)} | ||
\] | \] | ||
| − | + | С одной стороны получили условие на связь коэффициентов, с другой можем заметить, что имеет место единственная неподвижная точка — $$M(0,0, 0)$$ — неустойчива, при $$b > 1$$. | |
== Улучшение модели == | == Улучшение модели == | ||
Версия 20:33, 29 ноября 2023
Содержание
Модель динамики жуков
Жук Tribolium имеет три стадии развития: личинки — larva (L), куколки — pupa (P) и взрослая особь — adult (A). Динамическая модель численности жука, в которой естественно принять за единицу времени две недели, имеет вид: \begin{gather*} L \qquad P \qquad A \end{gather*}
\begin{equation} \label{sys1} \begin{cases} L_{t+1} = bA_t,\\ P_{t+1} = (1-\nu_L)L_t,\\ A_{t+1} = (1-\nu_P)P_t+(1+\nu_A)A_t, \end{cases} \end{equation} где $$\nu_L, \nu_P, \nu_A$$ — отношение количества погибающих естественным путем особей соответствующего вида к их общему числу, $$b$$ — коэффициент рождаемости (количество личинок, отложенных одним взрослым насекомым за единицу времени).
Исследование динамической системы
Определение 1. Неподвижная точка системы $$ u_{t+1}=f(u_t) $$ — это такая точка $$ N^* \in \mathbb{R} $$, что $$ f(N^*)=N^* $$.
Исследуем неподвижные точки системы (1) по определению:
\[ \begin{cases} L = bA,\\ P = (1-\nu_L)L,\\ A = (1-\nu_P)P +(1+\nu_A)A, \end{cases} \quad \Rightarrow \quad J = \begin{cases} L = bA,\\ P = (1-\nu_L)bA,\\ A = (1-\nu_P)(1-\nu_L)bA +(1+\nu_A)A, \end{cases}, \] \[ b = -\dfrac{(1+\nu_A)}{(1-\nu_P)(1-\nu_L)} \] С одной стороны получили условие на связь коэффициентов, с другой можем заметить, что имеет место единственная неподвижная точка — $$M(0,0, 0)$$ — неустойчива, при $$b > 1$$.
Улучшение модели
В реальности динамика популяции жука Tribolium имеет особенность. Когда популяция жуков достигает некоторой плотности, взрослые особи начинают поедать куколок и отложенные яйца (будущие личинки), сами личинки также поедают яйца. С учетом этих обстоятельств исходная модель приобретает вид:
\begin{equation} \label{sys2} \begin{cases} L_{t+1} = bA_te^{-c_{ll}A_t - c_{al}L_t},\\ P_{t+1} = (1-\nu_L)L_t,\\ A_{t+1} = (1-\nu_P)P_te^{-c_{pa}A_t}+(1+\nu_A)A_t, \end{cases} \end{equation} где $$\nu_{(\cdot)}$$ — отношение количества погибающих естественным путем особей соответствующего вида к их общему числу, $$b$$ — коэффициент рождаемости.
Новые обозначения:
$$~c_{al}$$ — количество личинок съеденных взрослыми особями.
$$~c_{ll}$$ — коэффициент каннибализма личинок.
$$~c_{ap}$$ — количество куколок съеденных взрослыми особями.
В ходе популяционных экспериментов и наблюдений были найдены значения параметров: \[ ~c_{al} = 0.012, ~c_{ll} = 0.009, ~c_{ap} = 0.004, ~\nu_L = 0.267, ~\nu_P = 0, ~\nu_A = 0.0036, ~b = 7.48 \]
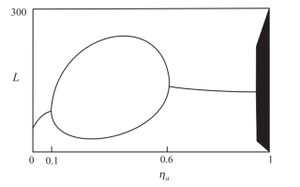
Биффуркационная диаграмма
Рассмотрим схематическое изображение бифуркационной диаграммы модели. Бифуркационный параметр — коэффициент смертности взрослых особей.
- Для относительно низких коэффициентов смертности численность личинок приходит в стационарное состояние (неподвижную точку).
- При $$\nu_A > 0.1$$ существует устойчивый цикл периода два, когда численность личинок колеблется между двумя существенно различными величинами - "вспышки численности".
- При $$\nu_A > 0.6$$ цикл исчезает, остается единственная устойчивая неподвижная точка.
- Для высоких значений коэффициента смертности решение имеет сложное непериодическое поведение.
Список литературы
1. Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии 2011.
2. Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2023.