Множество достижимости линейной управляемой системы, заданной при помощи ОДУ, без помехи. Внутренние оценки: различия между версиями
| (не показано 136 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''''Внутренние''''' [[Задача быстродействия "из множества во множество" | множества достижимости]] позволяют аппроксимировать это множество "изнутри", а также на основе полученной аппроксимации построить его приближенный вид. Также существуют [https://sawiki.cs.msu.ru/index.php | + | '''''Внутренние''''' оценки[[Задача быстродействия "из множества во множество" | множества достижимости]] позволяют аппроксимировать это множество "изнутри", а также на основе полученной аппроксимации построить его приближенный вид. Также существуют [https://sawiki.cs.msu.ru/index.php?title=%D0%9C%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE_%D0%B4%D0%BE%D1%81%D1%82%D0%B8%D0%B6%D0%B8%D0%BC%D0%BE%D1%81%D1%82%D0%B8_%D0%BB%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D0%BE%D0%B9_%D1%83%D0%BF%D1%80%D0%B0%D0%B2%D0%BB%D1%8F%D0%B5%D0%BC%D0%BE%D0%B9_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B,_%D0%B7%D0%B0%D0%B4%D0%B0%D0%BD%D0%BD%D0%BE%D0%B9_%D0%BF%D1%80%D0%B8_%D0%BF%D0%BE%D0%BC%D0%BE%D1%89%D0%B8_%D0%9E%D0%94%D0%A3,_%D0%B1%D0%B5%D0%B7_%D0%BF%D0%BE%D0%BC%D0%B5%D1%85%D0%B8._%D0%92%D0%BD%D0%B5%D1%88%D0%BD%D0%B8%D0%B5_%D0%BE%D1%86%D0%B5%D0%BD%D0%BA%D0%B8&action=edit&redlink=1 внешние оценки], которые позволяют аппроксимировать множество "снаружи". |
| − | == | + | ==Постановка задачи == |
| − | + | Рассмотрим линейное уравнение с непрерывными коэффициентами: | |
| + | |||
| + | \[ | ||
| + | \dot x(t) = A(t)x + B(t)u(t), t_{0} \leq t \leq t_{1}, | ||
| + | \] | ||
| + | где \( x(t) \in \mathbb{R^{n}}, A(t) \in \mathbb{R^{n \times n}}, B(t) \in \mathbb{R^{n \times m}}, u(.) \in L_{\infty}[t_{0},t_{1}]. \) | ||
| + | Предположим, что: \( u(t) \in \mathcal{P}(t) \subset \mathbb{R^{m}}, \) где \( \mathcal{P(.)}\) - непрерывное по Хаусдорфу многозначное отображение, при этом \(\mathcal{P(\tau)} \in conv\mathbb{R^{m}}. \) | ||
| + | Тогда получим задачу Коши: | ||
| + | |||
| + | \[ | ||
\begin{equation} | \begin{equation} | ||
| − | + | \begin{cases} | |
| − | + | \dot x(t) = A(t)x + B(t)u, t_{0} \leq t \leq t_{1}, \\ | |
| − | \dot x(t) = A(t)x | + | x(t_{0}) = x^{0}. |
| − | |||
| − | |||
\end{cases} | \end{cases} | ||
\end{equation} | \end{equation} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\] | \] | ||
| + | |||
| + | Под решением данной задачи будем понимать абсолютно непрерывную функцию \(x(.) \), которая удовлетворяет (1) почти всюду. Абсолютная непрерывность обязательна, так как в противном случае задача | ||
\[ | \[ | ||
| − | \ | + | \begin{equation} |
| + | \begin{cases} | ||
| + | \dot x(t) = 0, t_{0} \leq t \leq t_{1}, \\ | ||
| + | x(t_{0}) = 0 | ||
| + | \end{cases} | ||
| + | \end{equation} | ||
\] | \] | ||
| + | имеет, помимо тривиального, своим решением функцию Кантора. | ||
| − | == | + | ==Вспомогательные определения, теоремы и утверждения== |
В данном разделе даются необходимые определения и утверждения без доказательств, которые необходимы для решения соответствующей задачи. Основную информацию можно найти в [[Эллипсоид и его основные свойства | основной статье]]. | В данном разделе даются необходимые определения и утверждения без доказательств, которые необходимы для решения соответствующей задачи. Основную информацию можно найти в [[Эллипсоид и его основные свойства | основной статье]]. | ||
| + | ===Определение 1 === | ||
| + | '' Множеством достижимости в момент времени t из начальной позиции называется следующее множество точек: | ||
| + | \[ | ||
| + | \mathcal{X}[t] = \{x| \exists u(s), t_{0} \leq s \leq t \implies x(t,t_{0}, x^{0}) = x\} | ||
| + | \] | ||
| + | Начальная позиция: \((t_{0}, x^{0})\). | ||
| + | |||
===Утверждение 1=== | ===Утверждение 1=== | ||
| − | + | ''[[Выпуклое множество и его свойства | Выпуклое множество]] однозначно определяется своей [[Опорная функция множества | опорной функцией]]. | |
===Утверждение 2=== | ===Утверждение 2=== | ||
| − | + | ''[[Эллипсоид и его основные свойства | Эллипсоид]] с центром в точке q и матрицей Q в m-мерном вещественном пространстве можно определить как множество, построенное по направлению некоторого ненулевого вектора l:'' | |
| − | \[\mathcal{E}(q, Q) = \{x \in \mathbb{R}^m \:|\: \langle x,\,l \rangle \leq \langle l,\,q \rangle + \langle l,\,Ql \rangle^ | + | \[ |
| − | + | \mathcal{E}(q, Q) = \{x \in \mathbb{R}^m \:|\: \langle x,\,l \rangle \leq \langle l,\,q \rangle + \langle l,\,Ql \rangle^{1/2}\}, | |
| − | + | \] | |
| − | + | где \(l \in \mathbb{R^{n}} \). | |
| − | \ | ||
| − | === | + | ===Утверждение 3 === |
| − | + | ''Для любого [[Эллипсоид и его основные свойства | эллипсоида]] с центром в q, матрицей Q, и для любой матрицы A такой, что число ее столбов совпадает с числом строк Q, выполнено тождество:'' | |
\[ | \[ | ||
| − | + | A\mathcal{E}(q,Q) = \mathcal{E}(Aq, AQA'). | |
\] | \] | ||
| − | |||
==Внутренние эллипсоидальные оценки интеграла от многозначного отображения== | ==Внутренние эллипсоидальные оценки интеграла от многозначного отображения== | ||
| Строка 49: | Строка 62: | ||
Пусть даны эллипсоды: | Пусть даны эллипсоды: | ||
| − | \(\mathcal{E_{1}}(0, Q_{1})\) и \(\mathcal{E_{2}}(0, Q_{2})\), где \(Q_{1}\) и \(Q_{2}\) - некоторые положительно определенные матрицы(случай невырожденных эллипсоидов). | + | \(\mathcal{E_{1}}(0, Q_{1})\) и \(\mathcal{E_{2}}(0, Q_{2})\), где \(Q_{1}\) и \(Q_{2}\) - некоторые положительно определенные матрицы (случай невырожденных эллипсоидов). |
| + | |||
| + | Хотим найти \(\mathcal{E}\): \(\mathcal{E} \subseteq \mathcal{E_{1}}\) + \(\mathcal{E_{2}}\). | ||
| + | |||
| + | Введем обозначение: \( S[n] = (S_{1}, ... , S_{n}) \). | ||
| + | |||
| + | В качестве \(Q_-\) рассмотрим следующую матрицу: \(Q_-(S[2]) = (S_{1}Q^{1/2}_{1} + S_{2}Q^{1/2}_{2})^{'}(S_{1}Q^{1/2}+S_{2}Q^{1/2}_{2})\), где \(S_{1}\) и \(S_{2}\) - ортогональные матрицы: \(S'S\ = SS' = I\), \(I\) - единичная матрица. \(Q^{1/2}\) - квадратный корень из матрицы: у неотрицательно определенной матрицы \(Q\) \(\exists!\) квадратный корень, то есть симметричная матрица \(Q = Q^{1/2}Q^{1/2}\). | ||
| + | |||
| + | Покажем, что эллипсоид \(\mathcal{E_-}(0, Q_-) \) является внутренним по отношению к сумме \(\mathcal{E_{1}} + \mathcal{E_{2}}\), для этого оценим опорную функцию эллипсоида \(\mathcal{E_-}\). | ||
| + | |||
| + | \[ | ||
| + | \mathcal{\rho^{2}}(l|\mathcal{E_-}(0, Q_-)) = \langle l, (S_{1}Q^{1/2}_{1} + S_{2}Q^{1/2}_{2})'(S_{1}Q^{1/2}_{1} + S_{2}Q^{1/2}_{2})l \rangle = \langle l, Q_{1}l \rangle + \langle l, Q_{2}l \rangle + \langle S_{1}Q^{1/2}_{1}l, S_{2}Q^{1/2}_{2}l \rangle \leq | ||
| + | \] | ||
| + | в силу неравенства Коши-Буняковского: | ||
| + | \[ | ||
| + | \leq \langle l, Q_{1}l \rangle + \langle l, Q_{2}l \rangle + 2 \langle l, Q_{1}l \rangle ^{1/2} \langle l,Q_{2}l \rangle ^{1/2} = (\langle l, Q_{1}l \rangle ^{1/2} + \langle l, Q_{2}l \rangle ^{1/2})^{2} = \mathcal{\rho^{2}}(l| \mathcal{E_{1}} + \mathcal{E_{2}}) | ||
| + | \] | ||
| + | |||
| + | Заметим, что для \(l\) \(\neq\) \(0\) равенство достигается тогда и только тогда, когда аргументы скалярного произведения являются линейно зависимыми и сонаправленными, то есть: | ||
| + | \(S_{1}Q^{1/2}_{1}l = \lambda S_{2}Q^{1/2}_{2}l \), где \(\lambda > 0\). | ||
| + | |||
| + | В силу того, что мы можем повернуть вектор \(Q^{1/2}l\) на любой угол, для любого \(l\) всегда можно выбрать такую матрицу \(S\), что в неравенстве для опорных функций будет выполняться равенство и, следовательно, существует точка, в которой будет происходить касание эллипсоидов в силу вложенности одного множества в другое. | ||
| + | |||
| + | В случае \(m\) эллипсоидов поступим по аналогии: | ||
| + | \[ | ||
| + | Q_-(s[m]) = (\sum_{k=1}^{m} S_{k}Q^{1/2}_{k})'(\sum_{k=1}^{m} S_{k}Q^{1/2}_{k}). | ||
| + | \] | ||
| + | |||
| + | Тогда справедливо следующее вложение: \(\mathcal{E_-}(0, Q_-) \subseteq \sum_{k=1}^{m} \mathcal{E_{k}}(0, Q_{k}) \). Обоснование проводится с помощью опорной функции: | ||
| + | \[ | ||
| + | \mathcal{\rho^{2}}(l|\mathcal{E_-}(0, Q_-)) = \langle l, (\sum_{k=1}^{m} S_{k}Q^{1/2}_{2})^{1/2}(\sum_{k=1}^{m} S_{k}Q^{1/2}_{2})l \rangle = \sum_{k=1}^{m} \langle l, Q_{k}l \rangle + 2 \sum_{k=1}^{m-1} \sum_{s = k+1}^{m} \langle S_{k}Q^{1/2}_{2}l, S_{s}Q^{1/2}_{s}l \rangle \leq | ||
| + | \] | ||
| + | в силу неравенства Коши-Буняковского: | ||
| + | \[ | ||
| + | \leq \sum_{k=1}^{m} \langle \ Q_{k}l \rangle + 2 \sum_{k=1}^{m-1} \sum_{s = k+1}^{m} \langle l Q_{k}l \rangle ^{1/2} \langle l, Q_{s}l \rangle ^{1/2} = | ||
| + | (\sum_{k=1}^{m} \langle l, Q_{k}l \rangle ^{1/2})^{2} = \mathcal{\rho^{2}}(l| \sum_{k=1}^{m} \mathcal{E_{k}}) | ||
| + | \] | ||
| + | |||
| + | Имеет место следующее включение: \( \forall r =2,3...\) \(\sum_{k=1}^{r} \mathcal{E_{k}}(0, Q_{k}) = \bigcup_{S[r]} \mathcal{E_-} (0, Q_-(S[r])) \). | ||
| + | |||
| + | Центрированность эллипсоидов не является ограничением. Так, если: \(\mathcal{E_{k}(q_{k}, Q_{k})}_{k=1}^{m}\), то в качестве аппроксимирующего эллипсоида надо взять \( \mathcal{E_-}(q_-, Q_-) \), где \(q_- = \sum_{k=1}^{m} q_{k} \). Полученные результаты будут справедливы и в общем случае. | ||
| + | |||
| + | Перейдем к оценке для интеграла: | ||
| + | \[ | ||
| + | I = \mathcal{E}(q_{0}, Q_{0}) + \int_{t_{0}}^{t} \mathcal{E}(q(\tau), Q(\tau))d\tau. | ||
| + | \] | ||
| + | Для аппроксимации интеграла оценим частичную интегральную сумму: | ||
| + | \[ | ||
| + | I(N) = \mathcal{E}(q_{0}, Q_{0}) + \sum_{k=1}^{N} \delta _{k} \mathcal{E}(q(\tau_{k}), Q(\tau_{k})), | ||
| + | \] | ||
| + | где \(\delta_{k} = \tau_{k} - \tau_{k-1}, k = 1,...,N \), получаем \(\tau_{k} = \tau_{0} + \sum_{i=1}^{k}\delta_{k}, \ t_0 = \tau_0 < \tau_1 < \dots < \tau_k < \dots < \tau_N = t_1 \). | ||
| + | Если отображения \(q(\tau)\) и \(Q(\tau) \) непрерывные, то суммы частичного ряда сойдутся к значению интеграла. Очевидно также, что следует ожидать сходимости и аппроксимирующих эллипсоидов для интегральных сумм, то есть: | ||
| + | \(q_-(N) \to q_-, Q_-(N) \to Q_-\) при \(N \to \infty \). | ||
| + | |||
| + | Далее будем рассматривать только равномерные сетки. Получим формулы для центра и матрицы аппроксимирующего эллипсоида: | ||
| + | |||
| + | \[ | ||
| + | q_-(N) = q_{0} + \delta \sum_{k=1}^{N} q(\tau_{k}) | ||
| + | \] | ||
| − | + | ||
| + | \(Q_-(N) = Q'^{*}_{N}Q^{*}_{N},\) | ||
| + | |||
| + | где \(Q^{*}_{N} = S_{0}Q^{1/2}_{0} + \delta \sum_{k=1}^{N} S_{k} Q^{1/2}(\tau_{k}) \). | ||
| + | |||
| + | Равенство опорных функций достигается тогда и только тогда, когда: | ||
| + | \[ | ||
| + | S_{k}Q^{1/2}(\tau_{k})l = \lambda_{k}S_{0}Q^{1/2}_{0}l , \lambda_{k} > 0. | ||
| + | \] | ||
| + | |||
| + | Переходя к пределу, получим интегральное выражение для центра аппроксимирующего эллипсоида: | ||
| + | \[ | ||
| + | q_- = q_{0} + \int_{t_{0}}^{t} q(\tau)d\tau, | ||
| + | \] | ||
| + | а для его матрицы: | ||
| + | |||
| + | \[ | ||
| + | Q_- = Q'^{*}Q^{*}, | ||
| + | \] | ||
| + | |||
| + | где \( Q^{*} = (S_{0}Q^{1/2}_{0} + \int_{t_{0}}^{t} S(\tau)Q^{1/2}(\tau)d\tau). \) | ||
| + | |||
| + | Выбором \(S_{0}\) и \(S(\tau)\) из соотношений: | ||
| + | \[ | ||
| + | S(\tau)Q^{1/2}(\tau)l = \lambda(\tau)S_{0}Q^{1/2}_{0}l, \lambda(\tau) > 0, \forall \tau \in [t_{0}, t] | ||
| + | \] | ||
| + | мы всегда можем добиться касания. | ||
| + | |||
| + | Полученные выше интегральные уравнения для \(q_-\) и \(Q_-\) могут быть сведены к задаче Коши: | ||
| + | \[ | ||
| + | \begin{equation} | ||
| + | \begin{cases} | ||
| + | \dot q_- (t) = q(t), \\ | ||
| + | q_-(t_{0}) = q_{0} | ||
| + | \end{cases} | ||
| + | \end{equation} | ||
| + | \] | ||
| + | |||
| + | \[ | ||
| + | \begin{equation} | ||
| + | \begin{cases} | ||
| + | \dot Q_-(t) = \dot Q'^{*}(t) Q^{*}(t) + Q'^{*}(t)\dot Q^{*}(t), \\ | ||
| + | Q_-(t_{0}) = Q_{0}. | ||
| + | \end{cases} | ||
| + | \end{equation} | ||
| + | \] | ||
| + | |||
| + | А \(Q^{*}\) может быть найдено из следующего уравнения: | ||
| + | \[ | ||
| + | \begin{equation} | ||
| + | \begin{cases} | ||
| + | \dot Q^{*}(t) = S(t)Q^{1/2}(t), \\ | ||
| + | Q^{*}(t_{0}) = S_{0}Q^{1/2}_{0}. | ||
| + | \end{cases} | ||
| + | \end{equation} | ||
| + | \] | ||
== Внутренняя оценка для множества достижимости == | == Внутренняя оценка для множества достижимости == | ||
| Строка 58: | Строка 184: | ||
\label{2} | \label{2} | ||
\begin{cases} | \begin{cases} | ||
| − | \dot x = Ax + | + | \dot x = Ax + Bu, \\ |
x(t_0) \in \mathcal{E}_0(x_0, X_0), \\ | x(t_0) \in \mathcal{E}_0(x_0, X_0), \\ | ||
u(t) \in \mathcal{E}(p(t), P(t)). | u(t) \in \mathcal{E}(p(t), P(t)). | ||
\end{cases} | \end{cases} | ||
\end{equation} | \end{equation} | ||
| − | + | ||
| + | Требуется найти внутреннюю оценку для множества достижимости, которое может быть найдено в виде: | ||
\[ | \[ | ||
| − | \mathcal{X[t]} = X(t,t_0)\mathcal{E_0}(x_0, X_0) + \int^{t}_{t_0}X(t, \tau)\mathcal{E}(p(\tau), | + | \mathcal{X[t]} = X(t,t_0)\mathcal{E_0}(x_0, X_0) + \int^{t}_{t_0}X(t, \tau)B(\tau)\mathcal{E}(p(\tau), P(\tau)d{\tau} = \mathcal{E_0}(x_0, X(t, t_0)X_0X'(t, t_0)) + \int^{t}_{t_0} \mathcal{E}(p(\tau), X(t, \tau)B(\tau)P(\tau)X'(t, \tau) B'(\tau))d\tau. |
\] | \] | ||
| − | Для системы | + | Для системы (6) справедлива [[Формула Коши | формула Коши]]: |
\[ | \[ | ||
| − | x(t,t_0,x_0) = X(t,t_0)x_0 | + | x(t,t_0,x_0) = X(t,t_0)x_0 + \int^{t}_{t_0}X(t,\tau)B(\tau)u(\tau)d\tau, |
\] | \] | ||
| − | + | где \(X(t,\tau)\) - [[Фундаментальная матрица Коши | фундаментальная матрица]], удовлетворяющая системе: | |
\[ | \[ | ||
\left\{\begin{aligned} | \left\{\begin{aligned} | ||
| Строка 80: | Строка 207: | ||
Тогда для матриц аппроксимирующего эллипсоида: | Тогда для матриц аппроксимирующего эллипсоида: | ||
\[ | \[ | ||
| − | X\_ = (Q^{*}) | + | X\_ = (Q'^{*})Q^{*}, |
\] | \] | ||
| + | где \(Q^{*} = (S_0(X_{0})^{1/2}(X'(t, t_{0})) + \int^{t}_{t_0} S(\tau)P^{1/2}(\tau)X'(t, \tau)B'(\tau)d\tau)\). | ||
| + | |||
Касание достигается в случае: | Касание достигается в случае: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\[ | \[ | ||
| − | \ | + | S(\tau)P^{1/2}(\tau)X'(t,\tau)l(t) = \lambda(\tau)S_{0}X^{1/2}_{0}X'(t,t_{0})B'(\tau)l(t), \lambda(\tau) > 0, \forall \tau \in [t_{0},t]. |
| + | \] | ||
| + | |||
| + | В полученном равенстве есть зависимость от \(t\) и \(\tau\), то есть \(S(\tau) = S_{t}(\tau), \lambda(\tau) = \lambda_{t}(\tau) \). Таким образом, мы не можем для фиксированного \(l\) построить хорошей оценки, так как для каждого отдельного \(t\) придется делать пересчет, что влечет большую вычислительную сложность. Избавиться от этой трудности можно особым выбором зависимости \(l(\tau)\), а именно: | ||
| + | \[ | ||
| + | l^{*}(t) = X'(t_{0},t)l_{0} | ||
\] | \] | ||
| − | + | ||
| + | Подставим это в условие касания: | ||
\[ | \[ | ||
| − | + | S_{t}(\tau)P^{1/2}(\tau)B'(\tau)X'(t, \tau)X'(t_{0}, t)l_{0} = \lambda_{t}(\tau) S_{0}X^{1/2}_{0}X'(t,t_{0})X'(t_{0},t)l_{0} | |
\] | \] | ||
| − | + | ||
\[ | \[ | ||
| − | + | S_{t}(\tau)P^{1/2}(\tau)B'(\tau)X'(t_{0}, \tau)l_{0} = \lambda_{t}(\tau)S_{0}X^{1/2}_{0}I'l_{0} | |
\] | \] | ||
\[ | \[ | ||
| − | + | S_{t}(\tau)P^{1/2}(\tau)B'(\tau)X'(t_{0}, \tau)l_{0} = \lambda_{t}(\tau)S_{0}X^{1/2}_{0}l_{0} | |
\] | \] | ||
| − | + | Зависимость от \(t\) пропала, и нашу задачу для выбранной траектории можно свести к задаче Коши: | |
| + | \[ | ||
\begin{equation} | \begin{equation} | ||
| − | + | \begin{cases} | |
| − | \dot | + | \dot q_-(t) = Aq(t) + Bq(t), \\ |
| − | + | q_-(t_{0}) = q_{0}. | |
\end{cases} | \end{cases} | ||
\end{equation} | \end{equation} | ||
| + | \] | ||
| + | \[ | ||
\begin{equation} | \begin{equation} | ||
| − | + | \begin{cases} | |
| − | + | \dot X_-(t) = \dot Q'^{*}(t)Q^{*}(t) + Q'^{*}(t)\dot Q^{*}(t), \\ | |
| − | + | X_-(t_{0}) = X_{0} | |
| − | + | \end{cases} | |
\end{equation} | \end{equation} | ||
| + | \] | ||
| − | + | \(Q^{*}\) может быть найдено из системы уравнений: | |
| + | \[ | ||
\begin{equation} | \begin{equation} | ||
| − | + | \begin{cases} | |
| − | + | \dot Q^{*}(t) = S(t)P^{1/2}(t)B'(t) + Q^{*}(t)A'(t), \\ | |
| − | + | Q^{*}(t_{0}) = S_{0}X^{1/2}_{0}. | |
| − | + | \end{cases} | |
\end{equation} | \end{equation} | ||
| + | \] | ||
| + | |||
| + | ==Пример == | ||
| + | Рассмотрим систему (6) с параметрами | ||
| + | \[ | ||
| + | A = | ||
| + | \begin{pmatrix} | ||
| + | -1 & 0 & 0\\ | ||
| + | 0 & -4 & 0\\ | ||
| + | 0 & 0 & -1 | ||
| + | \end{pmatrix}, | ||
| + | \ \ | ||
| + | B = \begin{pmatrix} | ||
| + | 1 & 0 \\ | ||
| + | 0 & 1 \\ | ||
| + | 0 & 0 | ||
| + | \end{pmatrix}, | ||
| + | \ \ | ||
| + | x_0 = \begin{pmatrix} | ||
| + | 0 \\ | ||
| + | 0 \\ | ||
| + | 0 | ||
| + | \end{pmatrix}, | ||
| + | \ \ | ||
| + | X_0 = | ||
| + | \begin{pmatrix} | ||
| + | 1 & 0 & 0\\ | ||
| + | 0 & 20 & 0\\ | ||
| + | 0 & 0 & 1 | ||
| + | \end{pmatrix}, | ||
| + | \ \ | ||
| + | q = \begin{pmatrix} | ||
| + | 0 \\ | ||
| + | 0 | ||
| + | \end{pmatrix}, | ||
| + | \ \ | ||
| + | Q = \begin{pmatrix} | ||
| + | 2 & 1 \\ | ||
| + | 1 & 2 | ||
| + | \end{pmatrix}. | ||
| + | |||
| + | \] | ||
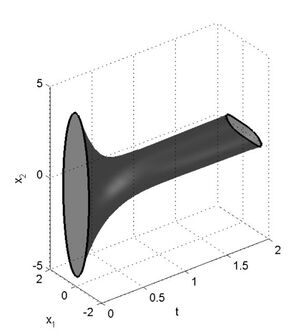
| + | Собственные значения матрицы \(A\) равны −1, −1, −4. Их отрицательность свидетельствует об устойчивости исследуемой системы. На иллюстрации | ||
| + | видно, что с течением времени \(t \) оценки внешние оценки множества достижимости стабилизируются (практически перестают меняться с течением времени). | ||
| + | |||
| + | [[Файл:Primer.jpg|мини|центр]] | ||
| + | |||
| + | |||
| + | Проекция оценки трубки достижимости на статическую трёхмерную плоскость. Двумерные сечения \( t = const\) представляют собой проекцию внутренней оценки множества достижимости. | ||
Текущая версия на 20:50, 25 декабря 2022
Внутренние оценки множества достижимости позволяют аппроксимировать это множество "изнутри", а также на основе полученной аппроксимации построить его приближенный вид. Также существуют внешние оценки, которые позволяют аппроксимировать множество "снаружи".
Содержание
Постановка задачи
Рассмотрим линейное уравнение с непрерывными коэффициентами:
\[ \dot x(t) = A(t)x + B(t)u(t), t_{0} \leq t \leq t_{1}, \] где \( x(t) \in \mathbb{R^{n}}, A(t) \in \mathbb{R^{n \times n}}, B(t) \in \mathbb{R^{n \times m}}, u(.) \in L_{\infty}[t_{0},t_{1}]. \) Предположим, что: \( u(t) \in \mathcal{P}(t) \subset \mathbb{R^{m}}, \) где \( \mathcal{P(.)}\) - непрерывное по Хаусдорфу многозначное отображение, при этом \(\mathcal{P(\tau)} \in conv\mathbb{R^{m}}. \) Тогда получим задачу Коши:
\[ \begin{equation} \begin{cases} \dot x(t) = A(t)x + B(t)u, t_{0} \leq t \leq t_{1}, \\ x(t_{0}) = x^{0}. \end{cases} \end{equation} \]
Под решением данной задачи будем понимать абсолютно непрерывную функцию \(x(.) \), которая удовлетворяет (1) почти всюду. Абсолютная непрерывность обязательна, так как в противном случае задача \[ \begin{equation} \begin{cases} \dot x(t) = 0, t_{0} \leq t \leq t_{1}, \\ x(t_{0}) = 0 \end{cases} \end{equation} \] имеет, помимо тривиального, своим решением функцию Кантора.
Вспомогательные определения, теоремы и утверждения
В данном разделе даются необходимые определения и утверждения без доказательств, которые необходимы для решения соответствующей задачи. Основную информацию можно найти в основной статье.
Определение 1
Множеством достижимости в момент времени t из начальной позиции называется следующее множество точек:
\[ \mathcal{X}[t] = \{x| \exists u(s), t_{0} \leq s \leq t \implies x(t,t_{0}, x^{0}) = x\} \] Начальная позиция: \((t_{0}, x^{0})\).
Утверждение 1
Выпуклое множество однозначно определяется своей опорной функцией.
Утверждение 2
Эллипсоид с центром в точке q и матрицей Q в m-мерном вещественном пространстве можно определить как множество, построенное по направлению некоторого ненулевого вектора l:
\[ \mathcal{E}(q, Q) = \{x \in \mathbb{R}^m \:|\: \langle x,\,l \rangle \leq \langle l,\,q \rangle + \langle l,\,Ql \rangle^{1/2}\}, \] где \(l \in \mathbb{R^{n}} \).
Утверждение 3
Для любого эллипсоида с центром в q, матрицей Q, и для любой матрицы A такой, что число ее столбов совпадает с числом строк Q, выполнено тождество:
\[ A\mathcal{E}(q,Q) = \mathcal{E}(Aq, AQA'). \]
Внутренние эллипсоидальные оценки интеграла от многозначного отображения
Построим внутреннюю эллипсоидальную оценку интеграла от многозначного отображения, где в качестве образа выступает эллипсоид.
Получим эллипсоидальную оценку для суммы двух эллипсоидов.
Пусть даны эллипсоды: \(\mathcal{E_{1}}(0, Q_{1})\) и \(\mathcal{E_{2}}(0, Q_{2})\), где \(Q_{1}\) и \(Q_{2}\) - некоторые положительно определенные матрицы (случай невырожденных эллипсоидов).
Хотим найти \(\mathcal{E}\): \(\mathcal{E} \subseteq \mathcal{E_{1}}\) + \(\mathcal{E_{2}}\).
Введем обозначение: \( S[n] = (S_{1}, ... , S_{n}) \).
В качестве \(Q_-\) рассмотрим следующую матрицу: \(Q_-(S[2]) = (S_{1}Q^{1/2}_{1} + S_{2}Q^{1/2}_{2})^{'}(S_{1}Q^{1/2}+S_{2}Q^{1/2}_{2})\), где \(S_{1}\) и \(S_{2}\) - ортогональные матрицы: \(S'S\ = SS' = I\), \(I\) - единичная матрица. \(Q^{1/2}\) - квадратный корень из матрицы: у неотрицательно определенной матрицы \(Q\) \(\exists!\) квадратный корень, то есть симметричная матрица \(Q = Q^{1/2}Q^{1/2}\).
Покажем, что эллипсоид \(\mathcal{E_-}(0, Q_-) \) является внутренним по отношению к сумме \(\mathcal{E_{1}} + \mathcal{E_{2}}\), для этого оценим опорную функцию эллипсоида \(\mathcal{E_-}\).
\[ \mathcal{\rho^{2}}(l|\mathcal{E_-}(0, Q_-)) = \langle l, (S_{1}Q^{1/2}_{1} + S_{2}Q^{1/2}_{2})'(S_{1}Q^{1/2}_{1} + S_{2}Q^{1/2}_{2})l \rangle = \langle l, Q_{1}l \rangle + \langle l, Q_{2}l \rangle + \langle S_{1}Q^{1/2}_{1}l, S_{2}Q^{1/2}_{2}l \rangle \leq \] в силу неравенства Коши-Буняковского: \[ \leq \langle l, Q_{1}l \rangle + \langle l, Q_{2}l \rangle + 2 \langle l, Q_{1}l \rangle ^{1/2} \langle l,Q_{2}l \rangle ^{1/2} = (\langle l, Q_{1}l \rangle ^{1/2} + \langle l, Q_{2}l \rangle ^{1/2})^{2} = \mathcal{\rho^{2}}(l| \mathcal{E_{1}} + \mathcal{E_{2}}) \]
Заметим, что для \(l\) \(\neq\) \(0\) равенство достигается тогда и только тогда, когда аргументы скалярного произведения являются линейно зависимыми и сонаправленными, то есть: \(S_{1}Q^{1/2}_{1}l = \lambda S_{2}Q^{1/2}_{2}l \), где \(\lambda > 0\).
В силу того, что мы можем повернуть вектор \(Q^{1/2}l\) на любой угол, для любого \(l\) всегда можно выбрать такую матрицу \(S\), что в неравенстве для опорных функций будет выполняться равенство и, следовательно, существует точка, в которой будет происходить касание эллипсоидов в силу вложенности одного множества в другое.
В случае \(m\) эллипсоидов поступим по аналогии: \[ Q_-(s[m]) = (\sum_{k=1}^{m} S_{k}Q^{1/2}_{k})'(\sum_{k=1}^{m} S_{k}Q^{1/2}_{k}). \]
Тогда справедливо следующее вложение: \(\mathcal{E_-}(0, Q_-) \subseteq \sum_{k=1}^{m} \mathcal{E_{k}}(0, Q_{k}) \). Обоснование проводится с помощью опорной функции: \[ \mathcal{\rho^{2}}(l|\mathcal{E_-}(0, Q_-)) = \langle l, (\sum_{k=1}^{m} S_{k}Q^{1/2}_{2})^{1/2}(\sum_{k=1}^{m} S_{k}Q^{1/2}_{2})l \rangle = \sum_{k=1}^{m} \langle l, Q_{k}l \rangle + 2 \sum_{k=1}^{m-1} \sum_{s = k+1}^{m} \langle S_{k}Q^{1/2}_{2}l, S_{s}Q^{1/2}_{s}l \rangle \leq \] в силу неравенства Коши-Буняковского: \[ \leq \sum_{k=1}^{m} \langle \ Q_{k}l \rangle + 2 \sum_{k=1}^{m-1} \sum_{s = k+1}^{m} \langle l Q_{k}l \rangle ^{1/2} \langle l, Q_{s}l \rangle ^{1/2} = (\sum_{k=1}^{m} \langle l, Q_{k}l \rangle ^{1/2})^{2} = \mathcal{\rho^{2}}(l| \sum_{k=1}^{m} \mathcal{E_{k}}) \]
Имеет место следующее включение: \( \forall r =2,3...\) \(\sum_{k=1}^{r} \mathcal{E_{k}}(0, Q_{k}) = \bigcup_{S[r]} \mathcal{E_-} (0, Q_-(S[r])) \).
Центрированность эллипсоидов не является ограничением. Так, если: \(\mathcal{E_{k}(q_{k}, Q_{k})}_{k=1}^{m}\), то в качестве аппроксимирующего эллипсоида надо взять \( \mathcal{E_-}(q_-, Q_-) \), где \(q_- = \sum_{k=1}^{m} q_{k} \). Полученные результаты будут справедливы и в общем случае.
Перейдем к оценке для интеграла: \[ I = \mathcal{E}(q_{0}, Q_{0}) + \int_{t_{0}}^{t} \mathcal{E}(q(\tau), Q(\tau))d\tau. \] Для аппроксимации интеграла оценим частичную интегральную сумму: \[ I(N) = \mathcal{E}(q_{0}, Q_{0}) + \sum_{k=1}^{N} \delta _{k} \mathcal{E}(q(\tau_{k}), Q(\tau_{k})), \] где \(\delta_{k} = \tau_{k} - \tau_{k-1}, k = 1,...,N \), получаем \(\tau_{k} = \tau_{0} + \sum_{i=1}^{k}\delta_{k}, \ t_0 = \tau_0 < \tau_1 < \dots < \tau_k < \dots < \tau_N = t_1 \). Если отображения \(q(\tau)\) и \(Q(\tau) \) непрерывные, то суммы частичного ряда сойдутся к значению интеграла. Очевидно также, что следует ожидать сходимости и аппроксимирующих эллипсоидов для интегральных сумм, то есть: \(q_-(N) \to q_-, Q_-(N) \to Q_-\) при \(N \to \infty \).
Далее будем рассматривать только равномерные сетки. Получим формулы для центра и матрицы аппроксимирующего эллипсоида:
\[ q_-(N) = q_{0} + \delta \sum_{k=1}^{N} q(\tau_{k}) \]
\(Q_-(N) = Q'^{*}_{N}Q^{*}_{N},\)
где \(Q^{*}_{N} = S_{0}Q^{1/2}_{0} + \delta \sum_{k=1}^{N} S_{k} Q^{1/2}(\tau_{k}) \).
Равенство опорных функций достигается тогда и только тогда, когда: \[ S_{k}Q^{1/2}(\tau_{k})l = \lambda_{k}S_{0}Q^{1/2}_{0}l , \lambda_{k} > 0. \]
Переходя к пределу, получим интегральное выражение для центра аппроксимирующего эллипсоида: \[ q_- = q_{0} + \int_{t_{0}}^{t} q(\tau)d\tau, \] а для его матрицы:
\[ Q_- = Q'^{*}Q^{*}, \]
где \( Q^{*} = (S_{0}Q^{1/2}_{0} + \int_{t_{0}}^{t} S(\tau)Q^{1/2}(\tau)d\tau). \)
Выбором \(S_{0}\) и \(S(\tau)\) из соотношений: \[ S(\tau)Q^{1/2}(\tau)l = \lambda(\tau)S_{0}Q^{1/2}_{0}l, \lambda(\tau) > 0, \forall \tau \in [t_{0}, t] \] мы всегда можем добиться касания.
Полученные выше интегральные уравнения для \(q_-\) и \(Q_-\) могут быть сведены к задаче Коши: \[ \begin{equation} \begin{cases} \dot q_- (t) = q(t), \\ q_-(t_{0}) = q_{0} \end{cases} \end{equation} \]
\[ \begin{equation} \begin{cases} \dot Q_-(t) = \dot Q'^{*}(t) Q^{*}(t) + Q'^{*}(t)\dot Q^{*}(t), \\ Q_-(t_{0}) = Q_{0}. \end{cases} \end{equation} \]
А \(Q^{*}\) может быть найдено из следующего уравнения: \[ \begin{equation} \begin{cases} \dot Q^{*}(t) = S(t)Q^{1/2}(t), \\ Q^{*}(t_{0}) = S_{0}Q^{1/2}_{0}. \end{cases} \end{equation} \]
Внутренняя оценка для множества достижимости
Рассматривается следующая задача динамики: \begin{equation} \label{2} \begin{cases} \dot x = Ax + Bu, \\ x(t_0) \in \mathcal{E}_0(x_0, X_0), \\ u(t) \in \mathcal{E}(p(t), P(t)). \end{cases} \end{equation}
Требуется найти внутреннюю оценку для множества достижимости, которое может быть найдено в виде: \[ \mathcal{X[t]} = X(t,t_0)\mathcal{E_0}(x_0, X_0) + \int^{t}_{t_0}X(t, \tau)B(\tau)\mathcal{E}(p(\tau), P(\tau)d{\tau} = \mathcal{E_0}(x_0, X(t, t_0)X_0X'(t, t_0)) + \int^{t}_{t_0} \mathcal{E}(p(\tau), X(t, \tau)B(\tau)P(\tau)X'(t, \tau) B'(\tau))d\tau. \] Для системы (6) справедлива формула Коши: \[ x(t,t_0,x_0) = X(t,t_0)x_0 + \int^{t}_{t_0}X(t,\tau)B(\tau)u(\tau)d\tau, \] где \(X(t,\tau)\) - фундаментальная матрица, удовлетворяющая системе: \[ \left\{\begin{aligned} & \frac{\partial X(t,\tau)}{\partial t} = A(t)X(t,\tau), \\ & X(\tau,\tau) = I. \end{aligned}\right. \] Тогда для матриц аппроксимирующего эллипсоида: \[ X\_ = (Q'^{*})Q^{*}, \] где \(Q^{*} = (S_0(X_{0})^{1/2}(X'(t, t_{0})) + \int^{t}_{t_0} S(\tau)P^{1/2}(\tau)X'(t, \tau)B'(\tau)d\tau)\).
Касание достигается в случае: \[ S(\tau)P^{1/2}(\tau)X'(t,\tau)l(t) = \lambda(\tau)S_{0}X^{1/2}_{0}X'(t,t_{0})B'(\tau)l(t), \lambda(\tau) > 0, \forall \tau \in [t_{0},t]. \]
В полученном равенстве есть зависимость от \(t\) и \(\tau\), то есть \(S(\tau) = S_{t}(\tau), \lambda(\tau) = \lambda_{t}(\tau) \). Таким образом, мы не можем для фиксированного \(l\) построить хорошей оценки, так как для каждого отдельного \(t\) придется делать пересчет, что влечет большую вычислительную сложность. Избавиться от этой трудности можно особым выбором зависимости \(l(\tau)\), а именно: \[ l^{*}(t) = X'(t_{0},t)l_{0} \]
Подставим это в условие касания: \[ S_{t}(\tau)P^{1/2}(\tau)B'(\tau)X'(t, \tau)X'(t_{0}, t)l_{0} = \lambda_{t}(\tau) S_{0}X^{1/2}_{0}X'(t,t_{0})X'(t_{0},t)l_{0} \]
\[ S_{t}(\tau)P^{1/2}(\tau)B'(\tau)X'(t_{0}, \tau)l_{0} = \lambda_{t}(\tau)S_{0}X^{1/2}_{0}I'l_{0} \]
\[ S_{t}(\tau)P^{1/2}(\tau)B'(\tau)X'(t_{0}, \tau)l_{0} = \lambda_{t}(\tau)S_{0}X^{1/2}_{0}l_{0} \]
Зависимость от \(t\) пропала, и нашу задачу для выбранной траектории можно свести к задаче Коши: \[ \begin{equation} \begin{cases} \dot q_-(t) = Aq(t) + Bq(t), \\ q_-(t_{0}) = q_{0}. \end{cases} \end{equation} \]
\[ \begin{equation} \begin{cases} \dot X_-(t) = \dot Q'^{*}(t)Q^{*}(t) + Q'^{*}(t)\dot Q^{*}(t), \\ X_-(t_{0}) = X_{0} \end{cases} \end{equation} \]
\(Q^{*}\) может быть найдено из системы уравнений: \[ \begin{equation} \begin{cases} \dot Q^{*}(t) = S(t)P^{1/2}(t)B'(t) + Q^{*}(t)A'(t), \\ Q^{*}(t_{0}) = S_{0}X^{1/2}_{0}. \end{cases} \end{equation} \]
Пример
Рассмотрим систему (6) с параметрами \[ A = \begin{pmatrix} -1 & 0 & 0\\ 0 & -4 & 0\\ 0 & 0 & -1 \end{pmatrix}, \ \ B = \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{pmatrix}, \ \ x_0 = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}, \ \ X_0 = \begin{pmatrix} 1 & 0 & 0\\ 0 & 20 & 0\\ 0 & 0 & 1 \end{pmatrix}, \ \ q = \begin{pmatrix} 0 \\ 0 \end{pmatrix}, \ \ Q = \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix}. \] Собственные значения матрицы \(A\) равны −1, −1, −4. Их отрицательность свидетельствует об устойчивости исследуемой системы. На иллюстрации видно, что с течением времени \(t \) оценки внешние оценки множества достижимости стабилизируются (практически перестают меняться с течением времени).
Проекция оценки трубки достижимости на статическую трёхмерную плоскость. Двумерные сечения \( t = const\) представляют собой проекцию внутренней оценки множества достижимости.