Множество разрешимости линейной управляемой системы, заданной при помощи ОДУ, без помехи. Внутренние оценки: различия между версиями
Polina (обсуждение | вклад) м (→Теорема 1) |
Polina (обсуждение | вклад) |
||
| (не показано 58 промежуточных версий 3 участников) | |||
| Строка 13: | Строка 13: | ||
\begin{cases} | \begin{cases} | ||
\dot x(t) = A(t)x(t) + B(t)u(t), \\ | \dot x(t) = A(t)x(t) + B(t)u(t), \\ | ||
| − | x( | + | x(t_1) \in \mathcal{X}_1, \\ |
u(t) \in \mathcal{P}(t), | u(t) \in \mathcal{P}(t), | ||
\end{cases} | \end{cases} | ||
\end{equation} | \end{equation} | ||
| − | где \(A(t) \in \mathbb{R}^{n \times n}, \ B(t) \in \mathbb{R}^{n \times m}, \ t \in [t_0, t_1],\) а множества \(\mathcal{X} | + | где \(A(t) \in \mathbb{R}^{n \times n}, \ B(t) \in \mathbb{R}^{n \times m}, \ t \in [t_0, t_1],\) а множества \(\mathcal{X}_1\) и \(\mathcal{P}(t)\) являются [[Эллипсоид и его основные свойства | эллипсоидами]]: |
\[ | \[ | ||
| − | \mathcal{X} | + | \mathcal{X}_1 = \mathcal{E}(x_1, X_1) \subset \mathbb{R}^n, |
\] | \] | ||
\[ | \[ | ||
\mathcal{P}(t) = \mathcal{E}(q(t), Q(t)) \subset \mathbb{R}^m. | \mathcal{P}(t) = \mathcal{E}(q(t), Q(t)) \subset \mathbb{R}^m. | ||
\] | \] | ||
| − | Тут \( | + | Тут \(x_1 \in \mathbb{R}^n, \ X_1 \in \mathbb{R}^{n\times n}, \ q(t) \in \mathbb{R}^m, \ Q(t) \in \mathbb{R}^{m\times m}\). Матрицы \(A(t), B(t), q(t), Q(t) \) - непрерывны на \([t_0, t_1] \). |
== Некоторые сведения об эллипсоидах == | == Некоторые сведения об эллипсоидах == | ||
| Строка 31: | Строка 31: | ||
==== Замечание 1 ==== | ==== Замечание 1 ==== | ||
| − | ''Т.к. [[Выпуклое множество и его свойства | выпуклое множество]] однозначно определяется своей [[Опорная функция множества | опорной функцией]], то [[Эллипсоид и его основные свойства | эллипсоид]] с центром в точке q и матрицей Q можно определить как множество | + | ''Т.к. [[Выпуклое множество и его свойства | выпуклое множество]] однозначно определяется своей [[Опорная функция множества | опорной функцией]], то [[Эллипсоид и его основные свойства | эллипсоид]] с центром в точке q и матрицей Q в n-мерном вещественном пространстве можно определить как множество:'' |
| − | \ | + | \begin{equation} \label{ellips_l} |
| + | \mathcal{E}(q, Q) = \{x \in \mathbb{R}^n \:|\: \langle x,\,l \rangle \leq \langle l,\,q \rangle + \langle l,\,Ql \rangle^\frac{1}{2}, \; \forall l \in \mathbb{R}^n\}, | ||
| + | \end{equation} | ||
==== Утверждение 1 ==== | ==== Утверждение 1 ==== | ||
| − | '' Для | + | '' Для любого эллипсоида с центром в q, матрицей Q, и для любой матрицы A, такой что число ее столбцов совпадает с числом строк Q, выполнено тождество:'' |
\[A\mathcal{E}(q,Q) = \mathcal{E}(Aq, AQA').\] | \[A\mathcal{E}(q,Q) = \mathcal{E}(Aq, AQA').\] | ||
| Строка 44: | Строка 46: | ||
\rangle} = \langle l,\,Aq \rangle + \sqrt{\langle l,\,AQA'l \rangle} = \rho(l\:|\:\mathcal{E}(Aq,AQA')). | \rangle} = \langle l,\,Aq \rangle + \sqrt{\langle l,\,AQA'l \rangle} = \rho(l\:|\:\mathcal{E}(Aq,AQA')). | ||
\] | \] | ||
| + | |||
| + | ==== Утверждение 2 ==== | ||
| + | ''Для [[Эллипсоид и его основные свойства | суммы эллипсоидов по Минковскому]] справедливо следующее выражение:'' | ||
| + | \[\mathcal{E}_-(q_-, Q_-) \subseteq \sum\limits^n_{i=1} \mathcal{E}(q_i, Q_i),\] | ||
| + | где \(q_- = \sum\limits_{i=1}^n q_i\), \(Q_- = Q'_*Q_*\), \(Q_* = \sum\limits_{i=1}^n S_i Q_i^\frac{1}{2}\), а \(S_i\) — некоторые [https://ru.wikipedia.org/wiki/Ортогональная_матрица ортогональные матрицы] | ||
| + | |||
| + | ===== Доказательство ===== | ||
| + | Для доказательства вложения, докажем неравенство для [[Опорная функция множества | опорных функций]]: | ||
| + | \[ | ||
| + | \rho(l\:|\:\mathcal{E}_-(q_-, Q_-)) = \left\langle l,\,\sum\limits_{i=1}^n q_i \right\rangle + \langle l,\,Q_*'Q_*l \rangle^{\frac{1}{2}} = | ||
| + | \sum\limits_{i=1}^n \langle l,\, q_i \rangle + \left\langle l,\,\left(\sum\limits_{i=1}^nS_iQ_i^{\frac{1}{2}}\right)' | ||
| + | \left(\sum\limits_{i=1}^nS_iQ_i^{\frac{1}{2}}\right) l \right\rangle^{\frac{1}{2}} = | ||
| + | \] | ||
| + | \[ | ||
| + | = \sum\limits_{i=1}^n \langle l,\, q_i \rangle + \sqrt{\sum\limits_{i=1}^n \langle l,\, Q_i \rangle + \sum\limits_{i=1}^n \sum\limits_{k=1, \\ k \neq i}^n \left\langle S_iQ_i^{\frac{1}{2}}l,\, S_kQ_k^{\frac{1}{2}}l \right\rangle} \stackrel{\text{н. К-Б}}{\leq} \sum\limits_{i=1}^n \langle l,\, q_i \rangle + | ||
| + | \] | ||
| + | \[ | ||
| + | + \sqrt{\sum\limits_{i=1}^n \langle l,\, Q_i \rangle + \sum\limits_{i=1}^n \sum\limits_{k=1, \\ k \neq i}^n \bigg|\bigg| S_iQ_i^{\frac{1}{2}}l \bigg|\bigg| \cdot \bigg|\bigg| S_kQ_k^{\frac{1}{2}}l \bigg|\bigg|} = \sum\limits_{i=1}^n \langle l,\, q_i \rangle + | ||
| + | \] | ||
| + | \[ | ||
| + | + \sqrt{\sum\limits_{i=1}^n \langle l,\, Q_i \rangle + \sum\limits_{i=1}^n \sum\limits_{k=1, \\ k \neq i}^n \sqrt{\left\langle S_iQ_i^{\frac{1}{2}}l,\, S_iQ_i^{\frac{1}{2}}l\right\rangle \left\langle S_kQ_k^{\frac{1}{2}}l,\, S_kQ_k^{\frac{1}{2}}l \right\rangle }}= | ||
| + | \] | ||
| + | \[ | ||
| + | = \sqrt{\sum\limits_{i=1}^n \langle l,Q_i \rangle + \sum\limits_{i=1}^n \sum\limits_{k=1, \\ k \neq i}^n \sqrt{\left\langle l,Q_il\right\rangle \left\langle l,Q_kl \right\rangle }} + | ||
| + | \] | ||
| + | \[ | ||
| + | + \sum\limits_{i=1}^n \langle l,q_i \rangle = \sum\limits_{i=1}^n \langle l,q_i \rangle + | ||
| + | \] | ||
| + | \[ | ||
| + | + \sqrt{\sum\limits_{i=1}^n \langle l,Q_i \rangle + 2\sum\limits_{i>k} \sqrt{\left\langle l,Q_il\right\rangle \left\langle l,Q_kl \right\rangle }} \stackrel{\text{св. оп. ф.}}{=} \rho\left(l\:\bigg|\:\sum\limits_{i=1}^n\mathcal{E}_i(q_i, Q_i)\right). | ||
| + | \] | ||
| + | |||
| + | Итак, вложенность доказана: | ||
| + | \[ | ||
| + | \rho(l\:|\:\mathcal{E}_-(q_-, Q_-)) \leq \rho\left(l\:\bigg|\:\sum\limits_{i=1}^n\mathcal{E}_i(q_i, Q_i)\right). | ||
| + | \] | ||
| + | |||
| + | При этом касание ("\(=\)") достигается в случае равенства в неравенстве Коши-Буняковского, т.е. когда система векторов \(\left\{S_iQ_i^{\frac{1}{2}}l\right\}\) линейно зависима, другими словами, если выполнено следующее тождество: | ||
| + | \begin{equation} | ||
| + | \label{kasanie} | ||
| + | S_iQ_i^{\frac{1}{2}}l = \lambda_iS_1Q_1l, \;\;\;\lambda_i = const > 0, \;\;\; \forall i = \overline{2,n} | ||
| + | \end{equation} | ||
| + | |||
==== Теорема 1 ==== | ==== Теорема 1 ==== | ||
''Для [[Эллипсоид и его основные свойства | суммы эллипсоидов по Минковскому]] можно получить внутреннюю эллипсоидальную оценку следующего вида:'' | ''Для [[Эллипсоид и его основные свойства | суммы эллипсоидов по Минковскому]] можно получить внутреннюю эллипсоидальную оценку следующего вида:'' | ||
\[ | \[ | ||
| − | \sum\limits^n_{i=1} \mathcal{E}(q_i, Q_i) = \bigcup_{\parallel l \parallel = 1} \mathcal{E}_-( | + | \sum\limits^n_{i=1} \mathcal{E}(q_i, Q_i) = \bigcup_{\parallel l \parallel = 1} \mathcal{E}_-(q_-, Q_-), |
\] | \] | ||
| − | где \(\ | + | где в правой части равенства рассматривается объединение по всем \(l\), таким, что \(\parallel l \!\parallel = 1\), эллипсоидов, представленных в виде \eqref{ellips_l}, с центром в \(q_- = \sum\limits_{i=1}^n q_i\) и матрицей \(Q_-(t) = Q'_*(t)Q_*(t)\), где \(Q_*(t) = \sum\limits_{i=1}^n S_i(t) Q_i^\frac{1}{2}(t)\), а \(S_i(t)\) — некоторые [https://ru.wikipedia.org/wiki/Ортогональная_матрица ортогональные матрицы]. |
===== Доказательство ===== | ===== Доказательство ===== | ||
| Строка 57: | Строка 102: | ||
== Внутренняя оценка множества разрешимости == | == Внутренняя оценка множества разрешимости == | ||
| − | Построим внутреннюю оценку множества разрешимости в задаче \eqref{1} | + | Построим внутреннюю оценку множества разрешимости в задаче \eqref{1}. |
Для системы \eqref{1} справедлива [[Формула Коши | формула Коши]]: | Для системы \eqref{1} справедлива [[Формула Коши | формула Коши]]: | ||
| Строка 80: | Строка 125: | ||
\lim_{N \rightarrow \infty} \sum^N_{i=1} \frac{t_1-t}{N} \cdot \mathcal{E} (X(t,\tau_i)B(\tau_i)q(\tau_i),\,X(t,\tau_i)B(\tau_i)Q(\tau_i)B'(\tau_i)X'(t,\tau_i)), | \lim_{N \rightarrow \infty} \sum^N_{i=1} \frac{t_1-t}{N} \cdot \mathcal{E} (X(t,\tau_i)B(\tau_i)q(\tau_i),\,X(t,\tau_i)B(\tau_i)Q(\tau_i)B'(\tau_i)X'(t,\tau_i)), | ||
\] | \] | ||
| − | то из '''теоремы 1''' можно получить следующую эллипсоидальную оценку для множества разрешимости | + | где \(\{\tau_i\}\) — разбиение отрезка \([t, t_1]\) на \(N\) частей (т.е. \(\tau_i = t+\frac{(t_1-t)i}{N}\)), то из '''теоремы 1''' можно получить следующую эллипсоидальную оценку для множества разрешимости: |
\[ | \[ | ||
| − | \mathcal{E}_- = \mathcal{E}\left(X(t,t_1)x_1 - \int^{t_1}_t X(t,\tau)B(\tau)q(\tau)d\tau,\,Q_-\right), | + | \mathcal{E}_- = \mathcal{E}_-(q_-, Q_-) = \mathcal{E}\left(X(t,t_1)x_1 - \int^{t_1}_t X(t,\tau)B(\tau)q(\tau)d\tau,\,Q_-\right), |
\] | \] | ||
где \(Q_-(t) = Q'_*(t)Q_*(t)\), и матрица \(Q_*(t)\) определяется следующим образом: | где \(Q_-(t) = Q'_*(t)Q_*(t)\), и матрица \(Q_*(t)\) определяется следующим образом: | ||
\[ | \[ | ||
| − | Q_*(t) = [X(t,t_1)X_1X'(t,t_1)]^\frac{1}{2} - \int^{t_1}_t | + | Q_*(t) = S(t_1)[X(t,t_1)X_1X'(t,t_1)]^\frac{1}{2} - \int^{t_1}_t S(\tau)[X(t,\tau)B(\tau)Q(\tau)B'(\tau)X'(t,\tau)]^\frac{1}{2}d\tau = |
| − | X_1^\frac{1}{2}X'(t,t_1) - \int^{t_1}_t | + | S(t_1) X_1^\frac{1}{2}X'(t,t_1) - \int^{t_1}_t S(\tau)Q^\frac{1}{2}(\tau)X'(t,\tau)d\tau, |
\] | \] | ||
| + | где \(S(·)\) – ортогональная матрица, которая в каждый момент времени \(t\) зависит от \(\tau\), а \(S(t_1) = I\). Причем, для любого \( l\) выбирается своя матрица \(S(·)\) так, чтобы в неравенстве для опорных функций \eqref{kasanie} выполнялось равенство, т.к. тогда будет существовать точка, в которой будет происходить касание эллипсоидов в силу вложенности одного множества в другое. В более явном виде эта зависимость показана в подразделе про [[ Множество разрешимости линейной управляемой системы, заданной при помощи ОДУ, без помехи. Внутренние оценки#Вычислительная часть | построение внутренней оценки]] . | ||
== Вычислительная часть == | == Вычислительная часть == | ||
| Строка 94: | Строка 140: | ||
=== Перебор по всем направлениям === | === Перебор по всем направлениям === | ||
| − | Как было показано в '''теореме 1''', при построении оценок нужно провести перебор по всем направлениям \(l\), таким что \(\parallel\! \ l \ \!\parallel\), т.е. провести перебор по \(n\)-мерной единичной сфере. Для этого удобно воспользоваться [https://ru.wikipedia.org/wiki/Гиперсфера гиперсферической системой координат] с единичным радиусом: | + | Как было показано в '''теореме 1''', при построении оценок нужно провести перебор по всем направлениям \(l\), таким что \(\parallel\! \ l \ \!\parallel = 1\), т.е. провести перебор по \(n\)-мерной единичной сфере. Для этого удобно воспользоваться [https://ru.wikipedia.org/wiki/Гиперсфера гиперсферической системой координат] с единичным радиусом: |
\[ | \[ | ||
\left\{\begin{aligned} | \left\{\begin{aligned} | ||
| Строка 107: | Строка 153: | ||
где \(\alpha_1,\,\alpha_2,\,\dots,\,\alpha_{n-1}\) равномерно распределены по отрезку \([0,\,\pi]\). Таким образом мы получаем равномерную сетку на сфере. | где \(\alpha_1,\,\alpha_2,\,\dots,\,\alpha_{n-1}\) равномерно распределены по отрезку \([0,\,\pi]\). Таким образом мы получаем равномерную сетку на сфере. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Построение проекции на плоскость === | === Построение проекции на плоскость === | ||
| Строка 150: | Строка 186: | ||
=== Оптимизация вычислений внутренней оценки === | === Оптимизация вычислений внутренней оценки === | ||
| − | Было показано, что внутренняя оценка | + | Было показано, что внутренняя оценка задается эллипсоидом: |
\[\mathcal{E}_- = \mathcal{E}\left(X(t,t_1)x_1 - \int^{t_1}_t X(t,\tau)B(\tau)q(\tau)d\tau,\,Q_*'(t)Q_*(t)\right),\] | \[\mathcal{E}_- = \mathcal{E}\left(X(t,t_1)x_1 - \int^{t_1}_t X(t,\tau)B(\tau)q(\tau)d\tau,\,Q_*'(t)Q_*(t)\right),\] | ||
| Строка 161: | Строка 197: | ||
| − | В соответствии с \( | + | В соответствии с \eqref{kasanie} из '''утверждения 2''' касание достигается в случае: |
| − | \ | + | \[ S(\tau)Q^{\frac{1}{2}}(\tau)X'(t,\tau)^{\frac{1}{2}}l(t) = \lambda(\tau) S_1 X_1^{\frac{1}{2}}X'(t,t_1)l(t), \] |
| + | где \( \lambda(\tau) > 0 \ \forall \tau \in [t_0,t_1].\) | ||
| + | Заметим, что в полученном равенстве есть зависимость от \(t\) и \(\tau\) , т.e. \( S(\tau) = S_t(\tau), \ \lambda(\tau) = \lambda_t(\tau)\). Таким образом мы не можем для фиксированного \(l\) построить хорошей оценки, так как для каждого отдельного \(t\) | ||
| + | придётся делать пересчет, что влечёт большую вычислительную сложность. Избавится от этой трудности | ||
| + | можно особым выбором зависимости \(l(t)\), а именно: | ||
| − | |||
\[l(t) = X'(t_1,t)l_1.\] | \[l(t) = X'(t_1,t)l_1.\] | ||
| Строка 184: | Строка 223: | ||
=== Построение внутренней оценки === | === Построение внутренней оценки === | ||
| − | Рассмотрим некоторое \(l_1 \in \pi\). Выразим из (\ref{s_without_t}) и \( \lambda = \frac{\langle l , | + | Рассмотрим некоторое \(l_1 \in \pi\). Выразим из (\ref{s_without_t}) и \( \lambda = \frac{\langle l , Q(\tau) l \rangle^{\frac{1}{2}}}{\langle l , Q_1 l \rangle^{\frac{1}{2}}} \) матрицу \(S(\tau)\): |
\[S(\tau)Q^\frac{1}{2}(\tau)B'(\tau)X'(t_1,\tau)l_1 = \frac{\langle l_1,\,X(t_1,\tau)B(\tau)QB'(\tau)X'(t_1,\tau)l_1\rangle^\frac{1}{2}}{\langle l_1,\,X_1l_1 \rangle^\frac{1}{2}}X^\frac{1}{2}_1l_1.\] | \[S(\tau)Q^\frac{1}{2}(\tau)B'(\tau)X'(t_1,\tau)l_1 = \frac{\langle l_1,\,X(t_1,\tau)B(\tau)QB'(\tau)X'(t_1,\tau)l_1\rangle^\frac{1}{2}}{\langle l_1,\,X_1l_1 \rangle^\frac{1}{2}}X^\frac{1}{2}_1l_1.\] | ||
| Строка 201: | Строка 240: | ||
| + | |||
| + | |||
Матрица \(S(\tau)\) вычисляется в соответствии с выражением: | Матрица \(S(\tau)\) вычисляется в соответствии с выражением: | ||
\[b = V_b \Sigma_b u_b = V_b (V_a' V_a) \Sigma_b u_b = V_b V_a' \cdot V_a \Sigma_b u_b = V_b V_a' \cdot V_a \left(\Sigma_a \frac{\sigma_b}{\sigma_a}\right) \left(u_a \frac{u_b}{u_a}\right) = \] | \[b = V_b \Sigma_b u_b = V_b (V_a' V_a) \Sigma_b u_b = V_b V_a' \cdot V_a \Sigma_b u_b = V_b V_a' \cdot V_a \left(\Sigma_a \frac{\sigma_b}{\sigma_a}\right) \left(u_a \frac{u_b}{u_a}\right) = \] | ||
| Строка 210: | Строка 251: | ||
\[\parallel\!\! \ a(\tau) \ \!\!\parallel = \parallel\!\! \ b(\tau) \ \!\!\parallel \Longrightarrow S(\tau) = V_b V'_a \frac{\sigma_b}{\sigma_a} \frac{u_b}{u_a}.\] | \[\parallel\!\! \ a(\tau) \ \!\!\parallel = \parallel\!\! \ b(\tau) \ \!\!\parallel \Longrightarrow S(\tau) = V_b V'_a \frac{\sigma_b}{\sigma_a} \frac{u_b}{u_a}.\] | ||
| + | где \(V_a,V_b\) ортогональные матрицы из [https://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D0%BD%D0%B3%D1%83%D0%BB%D1%8F%D1%80%D0%BD%D0%BE%D0%B5_%D1%80%D0%B0%D0%B7%D0%BB%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5 сингулярного разложения векторов ]: | ||
| + | \[ | ||
| + | a = V_a\Sigma_au_a, \ b = V_b\Sigma_bu_b. | ||
| + | \] | ||
Продифференцируем (\ref{q_with_star}): | Продифференцируем (\ref{q_with_star}): | ||
| Строка 217: | Строка 262: | ||
| − | Таким образом, матрица \(Q_*\) определяется следующей системой: | + | Таким образом, матрица \(Q_*(t)\) определяется следующей системой: |
\[ \left\{\begin{aligned} | \[ \left\{\begin{aligned} | ||
& \frac{\partial Q_*(t)}{\partial t} = Q_*(t)A'(t) - S(t)Q^\frac{1}{2}(t)B'(t), \\ | & \frac{\partial Q_*(t)}{\partial t} = Q_*(t)A'(t) - S(t)Q^\frac{1}{2}(t)B'(t), \\ | ||
| Строка 225: | Строка 270: | ||
| − | Матрицу \(Q_*(t)\) в системе '''Matlab''' можно найти с помощью численного интегрирования функцией '''ode45'''. По матрице \(Q_*\) построим матрицу \(Q_- = Q_*'Q_*\) и соответствующий эллипсоид \(\mathcal{E}_-\). При этом центр \(q_\varepsilon(t)\) эллипсоида \(\mathcal{E}_-\) удовлетворяет системе: | + | Матрицу \(Q_*(t)\) в системе '''Matlab''' можно найти с помощью численного интегрирования функцией '''ode45'''. По матрице \(Q_*(t)\) построим матрицу \(Q_-(t) = Q_*'(t)Q_*(t)\) и соответствующий эллипсоид \(\mathcal{E}_-\). При этом центр \(q_\varepsilon(t)\) эллипсоида \(\mathcal{E}_-\) удовлетворяет системе: |
\[ | \[ | ||
\left\{\begin{aligned} | \left\{\begin{aligned} | ||
| Строка 239: | Строка 284: | ||
В этой секции приведены некоторые возможные представления внутренних оценок множества разрешимости. | В этой секции приведены некоторые возможные представления внутренних оценок множества разрешимости. | ||
| − | Зеленым цветом отображается реальное множество разрешимости, а | + | Зеленым цветом отображается реальное множество разрешимости, а красным — внутренняя аппроксимация. |
=== Пример 1 === | === Пример 1 === | ||
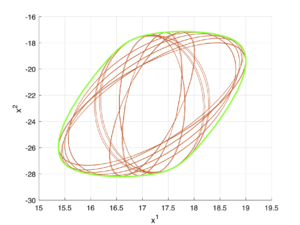
| + | [[Файл:Pr 1 set red.png|мини | Рис. 1: Пример внутренней оценки множества разрешимости]] | ||
\[A(t) = \begin{bmatrix} 1 & t \\ \sin{t} & -1 \end{bmatrix},\;\;B(t) = \begin{bmatrix} -1 & 0.5 \\ t & 10\sin{t} \end{bmatrix},\;\;Q(t) = \begin{bmatrix} 1 & -0.1t^2 \\ -0.1t^2 & 1 \end{bmatrix},\;\;X_1 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},\] | \[A(t) = \begin{bmatrix} 1 & t \\ \sin{t} & -1 \end{bmatrix},\;\;B(t) = \begin{bmatrix} -1 & 0.5 \\ t & 10\sin{t} \end{bmatrix},\;\;Q(t) = \begin{bmatrix} 1 & -0.1t^2 \\ -0.1t^2 & 1 \end{bmatrix},\;\;X_1 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},\] | ||
| − | \[x_1 = \begin{bmatrix} 20 \\ 0 \end{bmatrix},\;\;q(t) = \begin{bmatrix} 0 \\ 5 \end{bmatrix},\;\;t_1 = 1 | + | \[x_1 = \begin{bmatrix} 20 \\ 0 \end{bmatrix},\;\;q(t) = \begin{bmatrix} 0 \\ 5 \end{bmatrix},\;\;t_1 = 1.\] |
| − | + | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
=== Пример 2 === | === Пример 2 === | ||
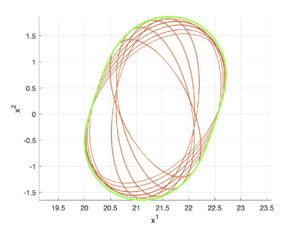
| − | \[A(t) = \begin{bmatrix} 1 & | + | [[Файл:Pr 2 set red.png|мини | Рис. 2: Пример внутренней оценки множества разрешимости]] |
| − | \[x_1 = \begin{bmatrix} 20 \\ 0 \end{bmatrix},\;\;q(t) = \begin{bmatrix} 0 \\ 5 \end{bmatrix},\;\;t_1 = 1 | + | \[A(t) = \begin{bmatrix} 1 & \sin{t} \\ 5 & t \end{bmatrix},\;\;B(t) = \begin{bmatrix} -1 & \cos{t} \\ t^2 & \sin{t} \end{bmatrix},\;\;Q(t) = \begin{bmatrix} 1 & 1 \\ t^2 & 1 \end{bmatrix},\;\;X_1 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},\] |
| + | \[x_1 = \begin{bmatrix} 20 \\ 0 \end{bmatrix},\;\;q(t) = \begin{bmatrix} 0 \\ 5 \end{bmatrix},\;\;t_1 = 1.\] | ||
| + | |||
| + | |||
| − | |||
[[Категория:ДП]] | [[Категория:ДП]] | ||
Текущая версия на 22:49, 18 декабря 2022
Внутренние оценки множества разрешимости позволяют аппроксимировать это множество "изнутри", а также на основе полученной аппроксимации построить его приближенный вид.
Если вместе со внутренними оценками построить и внешние, то можно точнее оценить, где находится истинное множество разрешимости, т.к. оно располагается между внутренними и внешними оценками.
В данной статье рассматривается только случай линейной управляемой системы, заданной при помощи ОДУ, без помехи. Также можно рассмотреть систему с помехой.
Содержание
Общий вид системы
Рассматривается линейная управляемая система дифференциальных уравнений без помехи: \begin{equation} \label{1} \begin{cases} \dot x(t) = A(t)x(t) + B(t)u(t), \\ x(t_1) \in \mathcal{X}_1, \\ u(t) \in \mathcal{P}(t), \end{cases} \end{equation} где \(A(t) \in \mathbb{R}^{n \times n}, \ B(t) \in \mathbb{R}^{n \times m}, \ t \in [t_0, t_1],\) а множества \(\mathcal{X}_1\) и \(\mathcal{P}(t)\) являются эллипсоидами: \[ \mathcal{X}_1 = \mathcal{E}(x_1, X_1) \subset \mathbb{R}^n, \] \[ \mathcal{P}(t) = \mathcal{E}(q(t), Q(t)) \subset \mathbb{R}^m. \] Тут \(x_1 \in \mathbb{R}^n, \ X_1 \in \mathbb{R}^{n\times n}, \ q(t) \in \mathbb{R}^m, \ Q(t) \in \mathbb{R}^{m\times m}\). Матрицы \(A(t), B(t), q(t), Q(t) \) - непрерывны на \([t_0, t_1] \).
Некоторые сведения об эллипсоидах
В этом разделе приводятся лишь те некоторые сведения об эллипсоидах, которые требуются в дальнейшем. Более подробную информацию об этих объектах можно получить в основной статье.
Замечание 1
Т.к. выпуклое множество однозначно определяется своей опорной функцией, то эллипсоид с центром в точке q и матрицей Q в n-мерном вещественном пространстве можно определить как множество:
\begin{equation} \label{ellips_l} \mathcal{E}(q, Q) = \{x \in \mathbb{R}^n \:|\: \langle x,\,l \rangle \leq \langle l,\,q \rangle + \langle l,\,Ql \rangle^\frac{1}{2}, \; \forall l \in \mathbb{R}^n\}, \end{equation}
Утверждение 1
Для любого эллипсоида с центром в q, матрицей Q, и для любой матрицы A, такой что число ее столбцов совпадает с числом строк Q, выполнено тождество:
\[A\mathcal{E}(q,Q) = \mathcal{E}(Aq, AQA').\]
Доказательство
Для доказательства равенства множеств, докажем равенство их опорных функций: \[ \rho(l\:|\:A\mathcal{E}(q,Q)) \stackrel{\text{св-во оп.ф.}}{=} \rho(A'l\:|\:\mathcal{E}(q,Q)) = \langle A'l,\,q \rangle + \sqrt{\langle A'l,\,QA'l \rangle} = \langle l,\,Aq \rangle + \sqrt{\langle l,\,AQA'l \rangle} = \rho(l\:|\:\mathcal{E}(Aq,AQA')). \]
Утверждение 2
Для суммы эллипсоидов по Минковскому справедливо следующее выражение: \[\mathcal{E}_-(q_-, Q_-) \subseteq \sum\limits^n_{i=1} \mathcal{E}(q_i, Q_i),\] где \(q_- = \sum\limits_{i=1}^n q_i\), \(Q_- = Q'_*Q_*\), \(Q_* = \sum\limits_{i=1}^n S_i Q_i^\frac{1}{2}\), а \(S_i\) — некоторые ортогональные матрицы
Доказательство
Для доказательства вложения, докажем неравенство для опорных функций: \[ \rho(l\:|\:\mathcal{E}_-(q_-, Q_-)) = \left\langle l,\,\sum\limits_{i=1}^n q_i \right\rangle + \langle l,\,Q_*'Q_*l \rangle^{\frac{1}{2}} = \sum\limits_{i=1}^n \langle l,\, q_i \rangle + \left\langle l,\,\left(\sum\limits_{i=1}^nS_iQ_i^{\frac{1}{2}}\right)' \left(\sum\limits_{i=1}^nS_iQ_i^{\frac{1}{2}}\right) l \right\rangle^{\frac{1}{2}} = \] \[ = \sum\limits_{i=1}^n \langle l,\, q_i \rangle + \sqrt{\sum\limits_{i=1}^n \langle l,\, Q_i \rangle + \sum\limits_{i=1}^n \sum\limits_{k=1, \\ k \neq i}^n \left\langle S_iQ_i^{\frac{1}{2}}l,\, S_kQ_k^{\frac{1}{2}}l \right\rangle} \stackrel{\text{н. К-Б}}{\leq} \sum\limits_{i=1}^n \langle l,\, q_i \rangle + \] \[ + \sqrt{\sum\limits_{i=1}^n \langle l,\, Q_i \rangle + \sum\limits_{i=1}^n \sum\limits_{k=1, \\ k \neq i}^n \bigg|\bigg| S_iQ_i^{\frac{1}{2}}l \bigg|\bigg| \cdot \bigg|\bigg| S_kQ_k^{\frac{1}{2}}l \bigg|\bigg|} = \sum\limits_{i=1}^n \langle l,\, q_i \rangle + \] \[ + \sqrt{\sum\limits_{i=1}^n \langle l,\, Q_i \rangle + \sum\limits_{i=1}^n \sum\limits_{k=1, \\ k \neq i}^n \sqrt{\left\langle S_iQ_i^{\frac{1}{2}}l,\, S_iQ_i^{\frac{1}{2}}l\right\rangle \left\langle S_kQ_k^{\frac{1}{2}}l,\, S_kQ_k^{\frac{1}{2}}l \right\rangle }}= \] \[ = \sqrt{\sum\limits_{i=1}^n \langle l,Q_i \rangle + \sum\limits_{i=1}^n \sum\limits_{k=1, \\ k \neq i}^n \sqrt{\left\langle l,Q_il\right\rangle \left\langle l,Q_kl \right\rangle }} + \] \[ + \sum\limits_{i=1}^n \langle l,q_i \rangle = \sum\limits_{i=1}^n \langle l,q_i \rangle + \] \[ + \sqrt{\sum\limits_{i=1}^n \langle l,Q_i \rangle + 2\sum\limits_{i>k} \sqrt{\left\langle l,Q_il\right\rangle \left\langle l,Q_kl \right\rangle }} \stackrel{\text{св. оп. ф.}}{=} \rho\left(l\:\bigg|\:\sum\limits_{i=1}^n\mathcal{E}_i(q_i, Q_i)\right). \]
Итак, вложенность доказана: \[ \rho(l\:|\:\mathcal{E}_-(q_-, Q_-)) \leq \rho\left(l\:\bigg|\:\sum\limits_{i=1}^n\mathcal{E}_i(q_i, Q_i)\right). \]
При этом касание ("\(=\)") достигается в случае равенства в неравенстве Коши-Буняковского, т.е. когда система векторов \(\left\{S_iQ_i^{\frac{1}{2}}l\right\}\) линейно зависима, другими словами, если выполнено следующее тождество: \begin{equation} \label{kasanie} S_iQ_i^{\frac{1}{2}}l = \lambda_iS_1Q_1l, \;\;\;\lambda_i = const > 0, \;\;\; \forall i = \overline{2,n} \end{equation}
Теорема 1
Для суммы эллипсоидов по Минковскому можно получить внутреннюю эллипсоидальную оценку следующего вида:
\[ \sum\limits^n_{i=1} \mathcal{E}(q_i, Q_i) = \bigcup_{\parallel l \parallel = 1} \mathcal{E}_-(q_-, Q_-), \] где в правой части равенства рассматривается объединение по всем \(l\), таким, что \(\parallel l \!\parallel = 1\), эллипсоидов, представленных в виде \eqref{ellips_l}, с центром в \(q_- = \sum\limits_{i=1}^n q_i\) и матрицей \(Q_-(t) = Q'_*(t)Q_*(t)\), где \(Q_*(t) = \sum\limits_{i=1}^n S_i(t) Q_i^\frac{1}{2}(t)\), а \(S_i(t)\) — некоторые ортогональные матрицы.
Доказательство
Можно найти в статье про внутренние оценки суммы двух эллипсоидов.
Внутренняя оценка множества разрешимости
Построим внутреннюю оценку множества разрешимости в задаче \eqref{1}.
Для системы \eqref{1} справедлива формула Коши: \[ x(t,t_1,x_1) = X(t,t_1)x_1 - \int^{t_1}_t X(t,\tau)B(\tau)u(\tau)d\tau, \] где \(X(t,\tau)\) - фундаментальная матрица, удовлетворяющая системе: \[ \left\{\begin{aligned} & \frac{\partial X(t,\tau)}{\partial t} = A(t)X(t,\tau), \\ & X(\tau,\tau) = I. \end{aligned}\right. \]
Т.к. множества \(\mathcal{X}_1, \mathcal{P}(t)\) — эллипсоиды, то с учетом утверждения 1 получим: \[ \mathcal{W}[t] = X(t, t_1)\mathcal{X}_1 - \int^{t_1}_t X(t,\tau)B(\tau)\mathcal{P}(\tau)d\tau =\mathcal{E}(X(t,t_1)x_1,\,X(t,t_1)X_1X'(t,t_1)) - \int^{t_1}_t \mathcal{E}(X(t,\tau)B(\tau)q(\tau),\,X(t,\tau)B(\tau)Q(\tau)B'(\tau)X'(t,\tau))d\tau. \]
Поскольку интеграл в полученном выражении представим как предел интегральных сумм \[ \lim_{N \rightarrow \infty} \sum^N_{i=1} \frac{t_1-t}{N} \cdot \mathcal{E} (X(t,\tau_i)B(\tau_i)q(\tau_i),\,X(t,\tau_i)B(\tau_i)Q(\tau_i)B'(\tau_i)X'(t,\tau_i)), \] где \(\{\tau_i\}\) — разбиение отрезка \([t, t_1]\) на \(N\) частей (т.е. \(\tau_i = t+\frac{(t_1-t)i}{N}\)), то из теоремы 1 можно получить следующую эллипсоидальную оценку для множества разрешимости: \[ \mathcal{E}_- = \mathcal{E}_-(q_-, Q_-) = \mathcal{E}\left(X(t,t_1)x_1 - \int^{t_1}_t X(t,\tau)B(\tau)q(\tau)d\tau,\,Q_-\right), \] где \(Q_-(t) = Q'_*(t)Q_*(t)\), и матрица \(Q_*(t)\) определяется следующим образом: \[ Q_*(t) = S(t_1)[X(t,t_1)X_1X'(t,t_1)]^\frac{1}{2} - \int^{t_1}_t S(\tau)[X(t,\tau)B(\tau)Q(\tau)B'(\tau)X'(t,\tau)]^\frac{1}{2}d\tau = S(t_1) X_1^\frac{1}{2}X'(t,t_1) - \int^{t_1}_t S(\tau)Q^\frac{1}{2}(\tau)X'(t,\tau)d\tau, \] где \(S(·)\) – ортогональная матрица, которая в каждый момент времени \(t\) зависит от \(\tau\), а \(S(t_1) = I\). Причем, для любого \( l\) выбирается своя матрица \(S(·)\) так, чтобы в неравенстве для опорных функций \eqref{kasanie} выполнялось равенство, т.к. тогда будет существовать точка, в которой будет происходить касание эллипсоидов в силу вложенности одного множества в другое. В более явном виде эта зависимость показана в подразделе про построение внутренней оценки .
Вычислительная часть
Перебор по всем направлениям
Как было показано в теореме 1, при построении оценок нужно провести перебор по всем направлениям \(l\), таким что \(\parallel\! \ l \ \!\parallel = 1\), т.е. провести перебор по \(n\)-мерной единичной сфере. Для этого удобно воспользоваться гиперсферической системой координат с единичным радиусом: \[ \left\{\begin{aligned} & x_1 = \sin{\alpha_1}\cdot\sin{\alpha_2}\cdot\,\dots\,\cdot\sin{\alpha_{n-1}}, \\ & x_2 = \cos{\alpha_1}\cdot\sin{\alpha_2}\cdot\,\dots\,\cdot\sin{\alpha_{n-1}}, \\ & x_3 = \cos{\alpha_2}\cdot\sin{\alpha_3}\cdot\,\dots\,\cdot\sin{\alpha_{n-1}}, \\ & \dots \\ & x_n = \cos{\alpha_{n-1}}, \end{aligned}\right. \]
где \(\alpha_1,\,\alpha_2,\,\dots,\,\alpha_{n-1}\) равномерно распределены по отрезку \([0,\,\pi]\). Таким образом мы получаем равномерную сетку на сфере.
Построение проекции на плоскость
Мы получили внутреннюю оценку множества разрешимости в виде объединения эллипсоидов. Теперь покажем, как спроецировать эллипс \(\mathcal{E}(q,Q)\) на плоскость \(\pi\), задаваемую неколлинеарными векторами \(l^0_1,l^0_2\).
Для начала, получим с помощью процесса ортогонализации пару ортогональных векторов в плоскости \(\pi\):
\[l_1 = l_1^0,\]
\[l_2 = l_2^0 - \frac{\langle l_2^0,\,l_1 \rangle}{\langle l_1,\,l_1 \rangle}l_1.\]
Теперь покажем, как спроектировать произвольную точку \(q\) на плоскость \(\pi\). Пусть \(pr_{\pi}(q) = \alpha l_1 + \beta l_2.\) Тогда:
\[
\left\{\begin{aligned}
& \langle q-pr_{\pi}(q),\,l_1 \rangle = 0, \\
& \langle q-pr_{\pi}(q),\,l_2 \rangle = 0.
\end{aligned}\right.
\Longrightarrow
\left\{\begin{aligned}
& \langle q-\alpha l_1 -\beta l_2,\,l_1 \rangle = 0, \\
& \langle q-\alpha l_1 -\beta l_2,\,l_2 \rangle = 0.
\end{aligned}\right.
\Longrightarrow
\left\{\begin{aligned}
& \alpha = \langle q,\,l_1 \rangle, \\
& \beta = \langle q,\,l_2 \rangle.
\end{aligned}\right.
\]
В соответствии с предыдущим пунктом, будем перебирать в плоскости \(\pi\) единичные векторы \(l\). Каждому из них сопоставим опорный вектор эллипсоида \(\mathcal{E}(q, Q)\) в соответствующем направлении. Спроектировав вершины опорных векторов на плоскость, получим искомую проекцию.
Оптимизация вычислений внутренней оценки
Было показано, что внутренняя оценка задается эллипсоидом: \[\mathcal{E}_- = \mathcal{E}\left(X(t,t_1)x_1 - \int^{t_1}_t X(t,\tau)B(\tau)q(\tau)d\tau,\,Q_*'(t)Q_*(t)\right),\]
где матрица \(Q_*(t)\) определяется следующим образом:
\begin{equation}
\label{q_with_star}
Q_*(t) = X_1^\frac{1}{2}X'(t,t_1) - \int^{t_1}_t S(\tau)Q^\frac{1}{2}(\tau)B'(\tau)X'(t,\tau)d\tau.
\end{equation}
В соответствии с \eqref{kasanie} из утверждения 2 касание достигается в случае:
\[ S(\tau)Q^{\frac{1}{2}}(\tau)X'(t,\tau)^{\frac{1}{2}}l(t) = \lambda(\tau) S_1 X_1^{\frac{1}{2}}X'(t,t_1)l(t), \]
где \( \lambda(\tau) > 0 \ \forall \tau \in [t_0,t_1].\)
Заметим, что в полученном равенстве есть зависимость от \(t\) и \(\tau\) , т.e. \( S(\tau) = S_t(\tau), \ \lambda(\tau) = \lambda_t(\tau)\). Таким образом мы не можем для фиксированного \(l\) построить хорошей оценки, так как для каждого отдельного \(t\)
придётся делать пересчет, что влечёт большую вычислительную сложность. Избавится от этой трудности
можно особым выбором зависимости \(l(t)\), а именно:
\[l(t) = X'(t_1,t)l_1.\]
Такая замена считается корректной. Поскольку \(X'(t_1,t)\) является невырожденным линейным оператором, он переводит \(r\)-мерное подпространство в \(r\)-мерное подпространство. Следовательно, векторы \(\{l_1\}\), лежащие в одной плоскости, после преобразования так же будут лежать в одной плоскости. При этом из непрерывности оператора следует, что окружность, на которой расположены векторы, так же перейдет в замкнутую кривую. Поскольку ноль перейдет в ноль, результатом преобразования будет что-то достаточно похожее на окружность.
Подставив замену в выражение для \(S\):
\[S(\tau)Q^\frac{1}{2}(\tau)B'(\tau)X'(t,\tau)X'(t_1,t)l_1 = \lambda(\tau)\cdot X_1^\frac{1}{2}X'(t,t_1)X'(t_1,t)l_1.\]
Тогда, с помощью полугруппового свойства фундаментальной матрицы, получим:
\begin{equation}
S(\tau)Q^\frac{1}{2}(\tau)B'(\tau)X'(t_1,\tau)l_1 = \lambda(\tau)\cdot X_1^\frac{1}{2}l_1.
\label{s_without_t}
\end{equation}
Теперь, в этом выражении матрица \(S(\tau)\) уже не зависит от \(t\), поэтому можно посчитать \(S(\tau)\) один раз для всего отрезка \([t,\,t_1]\).
Построение внутренней оценки
Рассмотрим некоторое \(l_1 \in \pi\). Выразим из (\ref{s_without_t}) и \( \lambda = \frac{\langle l , Q(\tau) l \rangle^{\frac{1}{2}}}{\langle l , Q_1 l \rangle^{\frac{1}{2}}} \) матрицу \(S(\tau)\): \[S(\tau)Q^\frac{1}{2}(\tau)B'(\tau)X'(t_1,\tau)l_1 = \frac{\langle l_1,\,X(t_1,\tau)B(\tau)QB'(\tau)X'(t_1,\tau)l_1\rangle^\frac{1}{2}}{\langle l_1,\,X_1l_1 \rangle^\frac{1}{2}}X^\frac{1}{2}_1l_1.\]
Обозначим для удобства:
\[a(\tau) = Q^\frac{1}{2}(\tau)B'(\tau)X'(t_1,\tau)l_1,\]
\[b(\tau) = \frac{\langle l_1,\,X(t_1,\tau)B(\tau)QB'(\tau)X'(t_1,\tau)l_1\rangle^\frac{1}{2}}{\langle l_1,\,X_1l_1 \rangle^\frac{1}{2}}X^\frac{1}{2}_1l_1.\]
Тогда, получим:
\[S(\tau)a(\tau) = b(\tau).\]
При этом для упрощения вычислений вектор \(b(\tau)\) удобнее считать как:
\[b(\tau) = \frac{\parallel\!\! \ a(\tau) \ \!\!\parallel}{\parallel\!\!\ X_1^\frac{1}{2}l_1 \ \!\!\parallel}X_1^\frac{1}{2}l_1.\]
Матрица \(S(\tau)\) вычисляется в соответствии с выражением:
\[b = V_b \Sigma_b u_b = V_b (V_a' V_a) \Sigma_b u_b = V_b V_a' \cdot V_a \Sigma_b u_b = V_b V_a' \cdot V_a \left(\Sigma_a \frac{\sigma_b}{\sigma_a}\right) \left(u_a \frac{u_b}{u_a}\right) = \]
\begin{equation}
= V_b V_a' \frac{\sigma_b}{\sigma_a}\frac{u_b}{u_a} \cdot V_a \Sigma_a u_a = \left(V_b V_a' \frac{\sigma_b}{\sigma_a}\frac{u_b}{u_a}\right)a.
\label{b_from_a}
\end{equation}
\[\parallel\!\! \ a(\tau) \ \!\!\parallel = \parallel\!\! \ b(\tau) \ \!\!\parallel \Longrightarrow S(\tau) = V_b V'_a \frac{\sigma_b}{\sigma_a} \frac{u_b}{u_a}.\]
где \(V_a,V_b\) ортогональные матрицы из сингулярного разложения векторов : \[ a = V_a\Sigma_au_a, \ b = V_b\Sigma_bu_b. \]
Продифференцируем (\ref{q_with_star}): \[\frac{\partial Q_*(t)}{\partial t} = X_1^\frac{1}{2}(A(t)X(t,t_1))' - \int^{t_1}_t S(\tau)Q^\frac{1}{2}(\tau)B'(\tau)(A(t)X(t,\tau))'d\tau - S(t)Q^\frac{1}{2}(t)B'(t) = \] \[= \left( X_1^\frac{1}{2}X'(t,t_1) - \int^{t_1}_t S(\tau)Q^\frac{1}{2}(\tau)B'(\tau)X'(t,\tau)d\tau \right)A'(t) - S(t)Q^\frac{1}{2}(t)B'(t) =\] \[= Q_*(t)A'(t) - S(t)Q^\frac{1}{2}(t)B'(t).\]
Таким образом, матрица \(Q_*(t)\) определяется следующей системой:
\[ \left\{\begin{aligned}
& \frac{\partial Q_*(t)}{\partial t} = Q_*(t)A'(t) - S(t)Q^\frac{1}{2}(t)B'(t), \\
& Q_*(t_1) = X_1^\frac{1}{2}.
\end{aligned}\right.
\]
Матрицу \(Q_*(t)\) в системе Matlab можно найти с помощью численного интегрирования функцией ode45. По матрице \(Q_*(t)\) построим матрицу \(Q_-(t) = Q_*'(t)Q_*(t)\) и соответствующий эллипсоид \(\mathcal{E}_-\). При этом центр \(q_\varepsilon(t)\) эллипсоида \(\mathcal{E}_-\) удовлетворяет системе:
\[
\left\{\begin{aligned}
& \frac{\partial q_\varepsilon}{\partial t} = A(t)q_\varepsilon(t) + B(t)q_\varepsilon(t), \\
& q_\varepsilon(t_1) = x_1.
\end{aligned}\right.
\]
Произведя перебор векторов \(l_1 \in \pi\), получим внутреннюю оценку.
Примеры вычислений
В этой секции приведены некоторые возможные представления внутренних оценок множества разрешимости.
Зеленым цветом отображается реальное множество разрешимости, а красным — внутренняя аппроксимация.
Пример 1
\[A(t) = \begin{bmatrix} 1 & t \\ \sin{t} & -1 \end{bmatrix},\;\;B(t) = \begin{bmatrix} -1 & 0.5 \\ t & 10\sin{t} \end{bmatrix},\;\;Q(t) = \begin{bmatrix} 1 & -0.1t^2 \\ -0.1t^2 & 1 \end{bmatrix},\;\;X_1 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},\] \[x_1 = \begin{bmatrix} 20 \\ 0 \end{bmatrix},\;\;q(t) = \begin{bmatrix} 0 \\ 5 \end{bmatrix},\;\;t_1 = 1.\]
Пример 2
\[A(t) = \begin{bmatrix} 1 & \sin{t} \\ 5 & t \end{bmatrix},\;\;B(t) = \begin{bmatrix} -1 & \cos{t} \\ t^2 & \sin{t} \end{bmatrix},\;\;Q(t) = \begin{bmatrix} 1 & 1 \\ t^2 & 1 \end{bmatrix},\;\;X_1 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},\] \[x_1 = \begin{bmatrix} 20 \\ 0 \end{bmatrix},\;\;q(t) = \begin{bmatrix} 0 \\ 5 \end{bmatrix},\;\;t_1 = 1.\]