Множество разрешимости линейной управляемой системы, заданной при помощи ОДУ, без помехи. Внутренние оценки: различия между версиями
Polina (обсуждение | вклад) |
Polina (обсуждение | вклад) м (Добавились графики) |
||
| Строка 246: | Строка 246: | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
=== Пример 2 === | === Пример 2 === | ||
| Строка 252: | Строка 259: | ||
\[A(t) = \begin{bmatrix} 1 & \sin{t} \\ 5 & t \end{bmatrix},\;\;B(t) = \begin{bmatrix} -1 & \cos{t} \\ t^2 & \sin{t} \end{bmatrix},\;\;Q(t) = \begin{bmatrix} 1 & 1 \\ t^2 & 1 \end{bmatrix},\;\;X_1 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},\] | \[A(t) = \begin{bmatrix} 1 & \sin{t} \\ 5 & t \end{bmatrix},\;\;B(t) = \begin{bmatrix} -1 & \cos{t} \\ t^2 & \sin{t} \end{bmatrix},\;\;Q(t) = \begin{bmatrix} 1 & 1 \\ t^2 & 1 \end{bmatrix},\;\;X_1 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},\] | ||
\[x_1 = \begin{bmatrix} 20 \\ 0 \end{bmatrix},\;\;q(t) = \begin{bmatrix} 0 \\ 5 \end{bmatrix},\;\;t_1 = 1,\;\;\varepsilon = 10^{-2}.\] | \[x_1 = \begin{bmatrix} 20 \\ 0 \end{bmatrix},\;\;q(t) = \begin{bmatrix} 0 \\ 5 \end{bmatrix},\;\;t_1 = 1,\;\;\varepsilon = 10^{-2}.\] | ||
| + | |||
[[Категория:ДП]] | [[Категория:ДП]] | ||
Версия 12:15, 7 декабря 2022
Внутренние оценки множества разрешимости позволяют аппроксимировать это множество "изнутри", а также на основе полученной аппроксимации построить его приближенный вид.
Если вместе со внутренними оценками построить и внешние, то можно точнее оценить, где находится истинное множество разрешимости, т.к. оно располагается между внутренними и внешними оценками.
В данной статье рассматривается только случай линейной управляемой системы, заданной при помощи ОДУ, без помехи. Также можно рассмотреть систему с помехой.
Содержание
Общий вид системы
Рассматривается линейная управляемая система дифференциальных уравнений без помехи: \begin{equation} \label{1} \begin{cases} \dot x(t) = A(t)x(t) + B(t)u(t), \\ x(t_0) \in \mathcal{X}_0, \\ u(t) \in \mathcal{P}(t), \end{cases} \end{equation} где \(A(t) \in \mathbb{R}^{n \times n}, \ B(t) \in \mathbb{R}^{n \times m}, \ t \in [t_0, t_1],\) а множества \(\mathcal{X}_0\) и \(\mathcal{P}(t)\) являются эллипсоидами: \[ \mathcal{X}_0 = \mathcal{E}(x_0, X_0) \subset \mathbb{R}^n, \] \[ \mathcal{P}(t) = \mathcal{E}(q(t), Q(t)) \subset \mathbb{R}^m. \] Тут \(x_0 \in \mathbb{R}^n, \ X_0 \in \mathbb{R}^{n\times n}, \ q(t) \in \mathbb{R}^m, \ Q(t) \in \mathbb{R}^{m\times m}\).
Некоторые сведения об эллипсоидах
В этом разделе приводятся лишь те некоторые сведения об эллипсоидах, которые требуются в дальнейшем. Более подробную информацию об этих объектах можно получить в основной статье.
Замечание 1
Т.к. выпуклое множество однозначно определяется своей опорной функцией, то эллипсоид с центром в точке q и матрицей Q можно определить как множество, построенное в направлении некоторого ненулевого вектора l:
\[\mathcal{E}(q, Q) = \{x \in \mathbb{R}^n \:|\: \langle x,\,l \rangle \leq \langle l,\,q \rangle + \langle l,\,Ql \rangle^\frac{1}{2}\},\]
Утверждение 1
Для любой матрицы A и любого эллипсоида с центром в точке q и матрицей Q выполнено тождество:
\[A\mathcal{E}(q,Q) = \mathcal{E}(Aq, AQA').\]
Доказательство
Для доказательства равенства множеств, докажем равенство их опорных функций: \[ \rho(l\:|\:A\mathcal{E}(q,Q)) \stackrel{\text{св-во оп.ф.}}{=} \rho(A'l\:|\:\mathcal{E}(q,Q)) = \langle A'l,\,q \rangle + \sqrt{\langle A'l,\,QA'l \rangle} = \langle l,\,Aq \rangle + \sqrt{\langle l,\,AQA'l \rangle} = \rho(l\:|\:\mathcal{E}(Aq,AQA')). \]
Теорема 1
Для суммы эллипсоидов по Минковскому можно получить внутреннюю эллипсоидальную оценку следующего вида:
\[ \sum\limits^n_{i=1} \mathcal{E}(q_i, Q_i) = \bigcup_{\parallel l \parallel = 1} \mathcal{E}_-(l), \] где \(\mathcal{E}_-(l) = \mathcal{E}(q_i, Q_-)\) — эллипсоид, построенный в направлении \(l\), с центром в \(q_i\) и матрицей \(Q_-(t) = Q'_*(t)Q_*(t)\), где \(Q_*(t) = \sum_{i=1}^n S_i(t) Q_i^\frac{1}{2}(t)\), а \(S_i(t)\) — некоторые ортогональные матрицы.
Доказательство
Можно найти в статье про внутренние оценки суммы двух эллипсоидов.
Внутренняя оценка множества разрешимости
Построим внутреннюю оценку множества разрешимости в задаче \eqref{1}. Без ограничения общности будем полагать \(m=n\) (при \(m<n\) можно расширить вектор \(u\) и матрицу \(B\), дополнив их соответствующими нулями).
Для системы \eqref{1} справедлива формула Коши: \[ x(t,t_1,x_1) = X(t,t_1)x_1 - \int^{t_1}_t X(t,\tau)B(\tau)u(\tau)d\tau, \] где \(X(t,\tau)\) - фундаментальная матрица, удовлетворяющая системе: \[ \left\{\begin{aligned} & \frac{\partial X(t,\tau)}{\partial t} = A(t)X(t,\tau), \\ & X(\tau,\tau) = I. \end{aligned}\right. \]
Т.к. множества \(\mathcal{X}_1, \mathcal{P}(t)\) — эллипсоиды, то с учетом утверждения 1 получим: \[ \mathcal{W}[t] = X(t, t_1)\mathcal{X}_1 - \int^{t_1}_t X(t,\tau)B(\tau)\mathcal{P}(\tau)d\tau =\mathcal{E}(X(t,t_1)x_1,\,X(t,t_1)X_1X'(t,t_1)) - \int^{t_1}_t \mathcal{E}(X(t,\tau)B(\tau)q(\tau),\,X(t,\tau)B(\tau)Q(\tau)B'(\tau)X'(t,\tau))d\tau. \]
Поскольку интеграл в полученном выражении представим как предел интегральных сумм \[ \lim_{N \rightarrow \infty} \sum^N_{i=1} \frac{t_1-t}{N} \cdot \mathcal{E} (X(t,\tau_i)B(\tau_i)q(\tau_i),\,X(t,\tau_i)B(\tau_i)Q(\tau_i)B'(\tau_i)X'(t,\tau_i)), \] , где \(\{\tau_i\}\) — разбиение отрезка \([t, t_1]\) на \(N\) частей (т.е. \(\tau_i = \frac{(t_1-t)i}{N}\)), то из теоремы 1 можно получить следующую эллипсоидальную оценку для множества разрешимости в направлении \(l\): \[ \mathcal{E}_- = \mathcal{E}\left(X(t,t_1)x_1 - \int^{t_1}_t X(t,\tau)B(\tau)q(\tau)d\tau,\,Q_-\right), \] где \(Q_-(t) = Q'_*(t)Q_*(t)\), и матрица \(Q_*(t)\) определяется следующим образом: \[ Q_*(t) = [X(t,t_1)X_1X'(t,t_1)]^\frac{1}{2} - \int^{t_1}_t S(\tau)[X(t,\tau)B(\tau)Q(\tau)B'(\tau)X'(t,\tau)]^\frac{1}{2}d\tau = X_1^\frac{1}{2}X'(t,t_1) - \int^{t_1}_t S(\tau)Q^\frac{1}{2}(\tau)B'(\tau)X'(t,\tau)d\tau. \] где \(S(\tau)\) ортогональная матрица.
Вычислительная часть
Перебор по всем направлениям
Как было показано в теореме 1, при построении оценок нужно провести перебор по всем направлениям \(l\), таким что \(\parallel\! \ l \ \!\parallel\), т.е. провести перебор по \(n\)-мерной единичной сфере. Для этого удобно воспользоваться гиперсферической системой координат с единичным радиусом: \[ \left\{\begin{aligned} & x_1 = \sin{\alpha_1}\cdot\sin{\alpha_2}\cdot\,\dots\,\cdot\sin{\alpha_{n-1}}, \\ & x_2 = \cos{\alpha_1}\cdot\sin{\alpha_2}\cdot\,\dots\,\cdot\sin{\alpha_{n-1}}, \\ & x_3 = \cos{\alpha_2}\cdot\sin{\alpha_3}\cdot\,\dots\,\cdot\sin{\alpha_{n-1}}, \\ & \dots \\ & x_n = \cos{\alpha_{n-1}}, \end{aligned}\right. \]
где \(\alpha_1,\,\alpha_2,\,\dots,\,\alpha_{n-1}\) равномерно распределены по отрезку \([0,\,\pi]\). Таким образом мы получаем равномерную сетку на сфере.
Построение проекции на плоскость
Мы получили внутреннюю оценку множества разрешимости в виде объединения эллипсоидов. Теперь покажем, как спроецировать эллипс \(\mathcal{E}(q,Q)\) на плоскость \(\pi\), задаваемую неколлинеарными векторами \(l^0_1,l^0_2\).
Для начала, получим с помощью процесса ортогонализации пару ортогональных векторов в плоскости \(\pi\):
\[l_1 = l_1^0,\]
\[l_2 = l_2^0 - \frac{\langle l_2^0,\,l_1 \rangle}{\langle l_1,\,l_1 \rangle}l_1.\]
Теперь покажем, как спроектировать произвольную точку \(q\) на плоскость \(\pi\). Пусть \(pr_{\pi}(q) = \alpha l_1 + \beta l_2.\) Тогда:
\[
\left\{\begin{aligned}
& \langle q-pr_{\pi}(q),\,l_1 \rangle = 0, \\
& \langle q-pr_{\pi}(q),\,l_2 \rangle = 0.
\end{aligned}\right.
\Longrightarrow
\left\{\begin{aligned}
& \langle q-\alpha l_1 -\beta l_2,\,l_1 \rangle = 0, \\
& \langle q-\alpha l_1 -\beta l_2,\,l_2 \rangle = 0.
\end{aligned}\right.
\Longrightarrow
\left\{\begin{aligned}
& \alpha = \langle q,\,l_1 \rangle, \\
& \beta = \langle q,\,l_2 \rangle.
\end{aligned}\right.
\]
В соответствии с предыдущим пунктом, будем перебирать в плоскости \(\pi\) единичные векторы \(l\). Каждому из них сопоставим опорный вектор эллипсоида \(\mathcal{E}(q, Q)\) в соответствующем направлении. Спроектировав вершины опорных векторов на плоскость, получим искомую проекцию.
Оптимизация вычислений внутренней оценки
Было показано, что внутренняя оценка в направлении \(l\) задается эллипсоидом: \[\mathcal{E}_- = \mathcal{E}\left(X(t,t_1)x_1 - \int^{t_1}_t X(t,\tau)B(\tau)q(\tau)d\tau,\,Q_*'(t)Q_*(t)\right),\]
где матрица \(Q_*(t)\) определяется следующим образом:
\begin{equation}
\label{q_with_star}
Q_*(t) = X_1^\frac{1}{2}X'(t,t_1) - \int^{t_1}_t S(\tau)Q^\frac{1}{2}(\tau)B'(\tau)X'(t,\tau)d\tau.
\end{equation}
В соответствии с \(S_iQ_i^{\frac{1}{2}}l = \lambda S_1 Q_1^{\frac{1}{2}}l, \forall i = \overline{2,n}\) (см. доказательство теоремы 1), матрица \(S(\tau)\) вычисляется из уравнения:
\[S(\tau)Q^\frac{1}{2}(\tau)B'(\tau)X'(t,\tau)l = \lambda(\tau)\cdot X_1^\frac{1}{2}X'(t,t_1)l.\]
Т.к. матрица \(S\), найденная из этого выражения, будет зависеть от \(t\), то обозначим: \[l(t) = X'(t_1,t)l_1.\]
Такая замена считается корректной. Поскольку \(X'(t_1,t)\) является невырожденным линейным оператором, он переводит \(r\)-мерное подпространство в \(r\)-мерное подпространство. Следовательно, векторы \(\{l_1\}\), лежащие в одной плоскости, после преобразования так же будут лежать в одной плоскости. При этом из непрерывности оператора следует, что окружность, на которой расположены векторы, так же перейдет в замкнутую кривую. Поскольку ноль перейдет в ноль, результатом преобразования будет что-то достаточно похожее на окружность.
Подставив замену в выражение для \(S\):
\[S(\tau)Q^\frac{1}{2}(\tau)B'(\tau)X'(t,\tau)X'(t_1,t)l_1 = \lambda(\tau)\cdot X_1^\frac{1}{2}X'(t,t_1)X'(t_1,t)l_1.\]
Тогда, с помощью полугруппового свойства фундаментальной матрицы, получим:
\begin{equation}
S(\tau)Q^\frac{1}{2}(\tau)B'(\tau)X'(t_1,\tau)l_1 = \lambda(\tau)\cdot X_1^\frac{1}{2}l_1.
\label{s_without_t}
\end{equation}
Теперь, в этом выражении матрица \(S(\tau)\) уже не зависит от \(t\), поэтому можно посчитать \(S(\tau)\) один раз для всего отрезка \([t,\,t_1]\).
Построение внутренней оценки
Рассмотрим некоторое \(l_1 \in \pi\). Выразим из (\ref{s_without_t}) и \( \lambda = \frac{\langle l , Q_i l \rangle^{\frac{1}{2}}}{\langle l , Q_1 l \rangle^{\frac{1}{2}}}, \forall i = \overline{2,n} \) матрицу \(S(\tau)\): \[S(\tau)Q^\frac{1}{2}(\tau)B'(\tau)X'(t_1,\tau)l_1 = \frac{\langle l_1,\,X(t_1,\tau)B(\tau)QB'(\tau)X'(t_1,\tau)l_1\rangle^\frac{1}{2}}{\langle l_1,\,X_1l_1 \rangle^\frac{1}{2}}X^\frac{1}{2}_1l_1.\]
Обозначим для удобства:
\[a(\tau) = Q^\frac{1}{2}(\tau)B'(\tau)X'(t_1,\tau)l_1,\]
\[b(\tau) = \frac{\langle l_1,\,X(t_1,\tau)B(\tau)QB'(\tau)X'(t_1,\tau)l_1\rangle^\frac{1}{2}}{\langle l_1,\,X_1l_1 \rangle^\frac{1}{2}}X^\frac{1}{2}_1l_1.\]
Тогда, получим:
\[S(\tau)a(\tau) = b(\tau).\]
При этом для упрощения вычислений вектор \(b(\tau)\) удобнее считать как:
\[b(\tau) = \frac{\parallel\!\! \ a(\tau) \ \!\!\parallel}{\parallel\!\!\ X_1^\frac{1}{2}l_1 \ \!\!\parallel}X_1^\frac{1}{2}l_1.\]
Утверждение 2
Для произвольных векторов \(a,b \in \mathbb{R}^{m\times 1}\), таких, что \(||a|| \,=\, ||b|| \), существует матрица ортогонального преобразования, переводящего \(a\) в \(b\).
Матрица \(S(\tau)\) вычисляется в соответствии с выражением:
\[b = V_b \Sigma_b u_b = V_b (V_a' V_a) \Sigma_b u_b = V_b V_a' \cdot V_a \Sigma_b u_b = V_b V_a' \cdot V_a \left(\Sigma_a \frac{\sigma_b}{\sigma_a}\right) \left(u_a \frac{u_b}{u_a}\right) = \]
\begin{equation}
= V_b V_a' \frac{\sigma_b}{\sigma_a}\frac{u_b}{u_a} \cdot V_a \Sigma_a u_a = \left(V_b V_a' \frac{\sigma_b}{\sigma_a}\frac{u_b}{u_a}\right)a.
\label{b_from_a}
\end{equation}
\[\parallel\!\! \ a(\tau) \ \!\!\parallel = \parallel\!\! \ b(\tau) \ \!\!\parallel \Longrightarrow S(\tau) = V_b V'_a \frac{\sigma_b}{\sigma_a} \frac{u_b}{u_a}.\]
где \(V_a,V_b\) ортогональные матрицы из сингулярного разложения векторов: \[ a = V_a\Sigma_au_a, \ b = V_b\Sigma_bu_b. \]
Продифференцируем (\ref{q_with_star}): \[\frac{\partial Q_*(t)}{\partial t} = X_1^\frac{1}{2}(A(t)X(t,t_1))' - \int^{t_1}_t S(\tau)Q^\frac{1}{2}(\tau)B'(\tau)(A(t)X(t,\tau))'d\tau - S(t)Q^\frac{1}{2}(t)B'(t) = \] \[= \left( X_1^\frac{1}{2}X'(t,t_1) - \int^{t_1}_t S(\tau)Q^\frac{1}{2}(\tau)B'(\tau)X'(t,\tau)d\tau \right)A'(t) - S(t)Q^\frac{1}{2}(t)B'(t) =\] \[= Q_*(t)A'(t) - S(t)Q^\frac{1}{2}(t)B'(t).\]
Таким образом, матрица \(Q_*(t)\) определяется следующей системой:
\[ \left\{\begin{aligned}
& \frac{\partial Q_*(t)}{\partial t} = Q_*(t)A'(t) - S(t)Q^\frac{1}{2}(t)B'(t), \\
& Q_*(t_1) = X_1^\frac{1}{2}.
\end{aligned}\right.
\]
Матрицу \(Q_*(t)\) в системе Matlab можно найти с помощью численного интегрирования функцией ode45. По матрице \(Q_*(t)\) построим матрицу \(Q_-(t) = Q_*'(t)Q_*(t)\) и соответствующий эллипсоид \(\mathcal{E}_-\). При этом центр \(q_\varepsilon(t)\) эллипсоида \(\mathcal{E}_-\) удовлетворяет системе:
\[
\left\{\begin{aligned}
& \frac{\partial q_\varepsilon}{\partial t} = A(t)q_\varepsilon(t) + B(t)q_\varepsilon(t), \\
& q_\varepsilon(t_1) = x_1.
\end{aligned}\right.
\]
Произведя перебор векторов \(l_1 \in \pi\), получим внутреннюю оценку.
Примеры вычислений
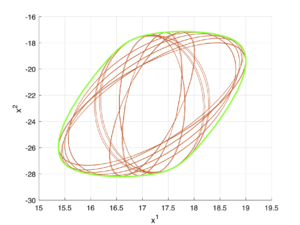
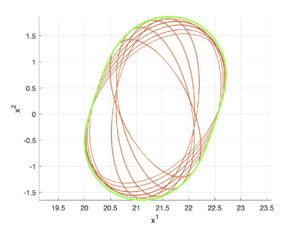
В этой секции приведены некоторые возможные представления внутренних оценок множества разрешимости.
Зеленым цветом отображается реальное множество разрешимости, а голубым — внутренняя аппроксимация.
Пример 1
\[A(t) = \begin{bmatrix} 1 & t \\ \sin{t} & -1 \end{bmatrix},\;\;B(t) = \begin{bmatrix} -1 & 0.5 \\ t & 10\sin{t} \end{bmatrix},\;\;Q(t) = \begin{bmatrix} 1 & -0.1t^2 \\ -0.1t^2 & 1 \end{bmatrix},\;\;X_1 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},\] \[x_1 = \begin{bmatrix} 20 \\ 0 \end{bmatrix},\;\;q(t) = \begin{bmatrix} 0 \\ 5 \end{bmatrix},\;\;t_1 = 1,\;\;\varepsilon = 10^{-2}.\]
Пример 2
\[A(t) = \begin{bmatrix} 1 & \sin{t} \\ 5 & t \end{bmatrix},\;\;B(t) = \begin{bmatrix} -1 & \cos{t} \\ t^2 & \sin{t} \end{bmatrix},\;\;Q(t) = \begin{bmatrix} 1 & 1 \\ t^2 & 1 \end{bmatrix},\;\;X_1 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},\] \[x_1 = \begin{bmatrix} 20 \\ 0 \end{bmatrix},\;\;q(t) = \begin{bmatrix} 0 \\ 5 \end{bmatrix},\;\;t_1 = 1,\;\;\varepsilon = 10^{-2}.\]